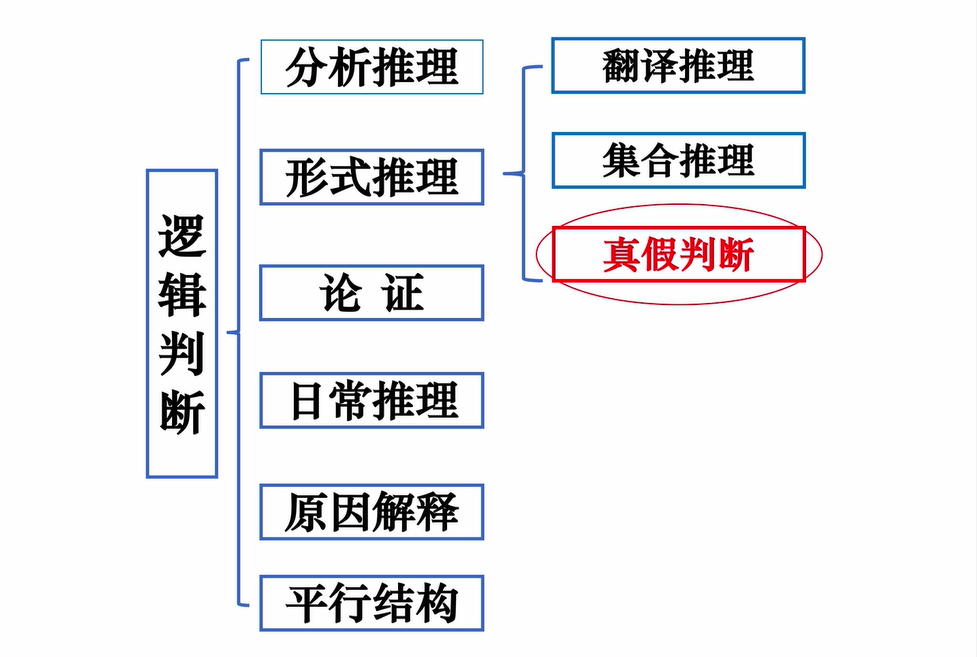
Appearance
题目识别
题干中:有若干论断
题设中:一真/一假、两真/两假

解题原则
先判断真假,后推理结论。
为真——直接用
为假——反着用
矛盾关系
口诀:首先找矛盾、关键是其余
使用方法
1.首先找到矛盾,绕过矛盾看其余
2.条件一假,假话在矛盾中,其余全真
条件一真,真话在矛盾中,其余全假
矛盾关系:
必有一真,必有一假
同真不矛盾,同假不矛盾
六对矛盾:
A & -A
所有S都是P & 有的S不是P (所有都 & 有的不)
例:所有小伙伴都是男生
有的小伙伴不是男生
所有S都不是P & 有的S是P (所有都不 & 有的是)
例:所有的小伙伴都不是胖子
有的小伙伴是胖子
P → Q & P 且 -Q
例:如果考上公务员,那么我就嫁给你
考上公务员 → 嫁给你
①考上了,而且嫁给你了
②考上了,但是没嫁给你③没考上,但嫁给你了
④没考上,也没嫁给你
A且B & -A 或 -B
A 或 B & -A 且 -B
【例1】甲、乙、丙、丁四人在一起工作,有人趁别人不在意拿走一件物品藏匿起来。领导发现后问是谁干的,甲说:“是乙干的”;乙说:“不是我干的”;丙说:“不是我干的”;丁没表态。现知三人中只有一个人说的是真话。
甲:乙
乙:-乙
丙:-丙
甲、乙一真一假
由此可以推出,拿走物品藏匿起来的人是( )。
A.乙
B.丁
C.丙
D.甲
TIP
解题思路回顾:
第一步:找矛盾
第二步:看其余
①一假余真;其余为真,直接用(代入推理)
②一真余假;其余为假,反着用(矛盾关系)
【例2】甲、乙、丙、丁四人在一起议论本班同学申请银行助学贷款的情况。
甲:“我班所有的同学都申请了助学货款。”
乙:“如果班长申请了助学贷款,那么学习委员就没有申请。”
丙:“班长申请了助学贷款。”
丁:“我班有人没有申请助学贷款。”
甲:所有都
乙:班长 → -学委
丙:班
丁:有的不
甲、丁矛盾,乙、丙为真
已知四人中只有一个人说假话,则可推出以下哪项结论?( )
A.甲说假话,学习委员没申请
B.乙说假话,班长没申请
C.丙说假话,学习委员没申请
D.丁说假话,学习委员申请了
【例3】某大学积极引导大学生开展暑期社会实践活动,取得显著效果。学校和某乡镇联合选拔两位品学兼优的学生到该乡镇担任村官,多方考核之后,甲乙丙丁四人在一起讨论入选的可能性:
甲说:“我不会入选。”
乙说:“如果我入选,则丙会入选。”
丙说:“如果乙入选,则丁会入选。”
丁说:“乙会入选但丙不会入选。”
甲:-甲
乙:乙 → 丙
丙:乙 → 丁
乙 且 -丁
丁:乙 且 -丙
乙、丁矛盾:一真一假,其余为假
如果四人中只有一人猜对,则下列哪项判断必然为真?( )
A.甲、乙会入选
B.甲、丁会入选
C.乙、丙会入选
D.乙、丁会入选
反对关系
口诀:其次找反对,关键是其余
使用方法
1.没有矛盾找反对,绕过反对看其余
2.条件一真,找到“有的”和“有的不”,其余全假
条件一假,找到“所有都”和“所有都不”,其余全真
两对反对:
所有S都是P & 所有S都不是P
| 所有人都戴眼镜 | 所有人都不戴眼镜 | |
|---|---|---|
| ①全戴 | √ | × |
| ②全不戴 | × | √ |
| ③有的戴有的不戴 | × | × |
TIP
两个所有,必有一假
有的S是P & 有的S不是P
| 有的人都戴眼镜 | 有的人都不戴眼镜 | |
|---|---|---|
| ①全戴 | √ | × |
| ②全不戴 | × | √ |
| ③有的戴有的不戴 | √ | √ |
TIP
两个有的,必有一真
【例4】甲、乙、丙、丁四同学在一起议论本班参加A活动的情况。
甲说:我班所有同学都参加了;
乙说:如果张帆没参加,那么李航也没参加;
丙说:李航参加了;
丁说:我班所有同学都没有参加。
甲:所有都
乙:-张 → -李
丙:李
丁:所有都不
甲、丁为反对关系:必有一假
已知四人中只有一人说的不正确,由此可见( )。
A.甲说的不正确,张帆没参加
B.乙说的不正确,张帆参加了
C.丙说的不正确,张帆没参加
D.丁说的不正确,张帆参加了
【例5】某律师事务所共有12名工作人员。
(1)有人会使用计算机;
(2)有人不会使用计算机;
(3)所长不会使用计算机。
①有的是
②有的不
③-所长
①②是反对关系:必有一真
则③为假话:③ → 所长
则①为真话,②为假话
② → 所有都
这三个命题中只有一个是真的,以下哪项正确地表示了律师事务所会使用计算机的人数?( )
A.12人都会使用
B.12人没人会使
C.仅有一人会使用
D.不能确定
秒杀口诀:“ 欺软怕硬”
“两个有的”口诀:条件只有一真,找点名那句,反着它说,人称变所有。
【例1】(1)“有的同学是党员”;
(2)“有的同学不是党员”;
(3)“涛涛是党员”。
例1中出现两个“有的”,“有的”的表述很“软”,很委婉,因此可以找点名的那句,即第(3)句点了涛涛的名,反着它说,人称变所有,即正确答案应该是“所有同学都不是党员”。
“两个所有”口诀:条件只有一假,找点名那句,顺着它说,人称变所有。
【例2】(1)“所有同学都是党员”;
(2)“所有同学都不是党员”;
(3)“涛涛是党员”。
例2中出现两个“所有”,“所有”的表述很“硬”,因此可以找点名的那句,即第(3)句点了涛涛的名,顺着它说,人称变所有,即正确答案应该是“所有同学都是党员”。
推出关系
口诀:两真两假,想推出
使用方法
第一步:找矛盾关系,一真一假。
第二步:另外两个命题也是一真一假,然后假设。
如果另外两个命题是“A”和“A或B”,那么如果假设“A”为真,则“A或B”也为真,不符合“一真一假”,故假设错误,所以“A”为假,“A或B”为真。
如果另外两个命题是“A”和“A且B”,那么如果假设“A”为假,则“A且B”也为假,不符合“一真一假”,故假设错误,所以“A”为真,“A且B”为假。
推出本质:为真逻辑必然性
两串推出:
所有 → 某个 → 有的
A 且 B → A(B) → A 或 B
【例6】关于一个班的英语六级通过情况有如下陈述:
(1)班长通过了
(2)该班所有人都通过了
(3)有些人通过了
(4)有些人没有通过
①班长
②所有都
③有的是
④有的不
②④为矛盾关系,必有一真一假
则:①③必有一真一假
根据:某个 → 有的,则①为真,③也为真
则:①为假 ③为真 排除B、C、D,选择A
经过详细调查,发现上述断定只有两个是正确的。可见( )。
A.该班有人通过了,但也有人没有通过
B.班长通过了
C.所有人都通过了
D.所有人都没有通过
【例7】英语六级考试结束后,关于王刚、刘超二人是否能通过考试,宿舍同学有如下讨论:
王刚说:或者我能通过,或者刘超能通过,或者我和刘超都能通过。
李强说:王刚一定能通过。
杨帆说:刘超能通过。
赵进说:王刚没有可能通过。
①王或刘
②王
③刘
④-王
②④矛盾,必有一真一假
则:①③必有一真一假
若③为真,则①为真
则:③为假,①为真
①或关系否一推一,刘没通过,王通过,选择C
考试成绩出来后,证明四人的话有两人说的是真的,两人说的是假的。
根据以上陈述,可推出以下哪项?( )
A.王刚、刘超都通过了
B.王刚、刘超都没通过
C.王刚通过了,刘超没通过
D.刘超通过了,王刚没通过
假设法
若无矛盾关系和反对关系,可以考虑假设法
【例】青少年高校科学营旨在充分利用重点大学的科技教育资源,激发青少年对科学的兴趣,培养青少年的科学精神、创新意识和实践能力。班主任鼓励甲、乙、丙、丁四位同学报名参加暑假举行的科学营。几天后班主任向这四位同学询问录取的情况,他们的回答如下:
甲:乙被科学营录取了;
乙:丙被科学营录取了;
丙:甲或者乙被科学营录取了;
丁:乙或者丙被科学营录取了。
经过班主任调查,发现只有一位同学的回答与事实相符。
根据以上陈述,下列哪项为假?
A.丙说的是真话
B.乙没有被科学营录取
C.被科学营录取的不是甲
D.丁说的是假话
本题题干没有任何矛盾关系和反对关系,故考虑假设法。
若甲的话为真,则丙和丁的话都为真;
若乙的话为真,则丁的话也为真。
但四人中只有一人的回答与事实相符,则甲和乙的话均为假,即乙和丙都没有被录取。
乙且丙均没有被录取,故丁的话也为假,因只有一人的话为真,故丙的话为真,即甲或乙被录取,而乙没有被录取,则可知甲一定被录取,故C项为假。
综合练习
【例8】驾照考试期间,每次“路考”都有近百人参加,且有通过的比率。甲乙丙丁猜测,四人中谁能通过路考。
甲:如果李娜能通过,那么刑燕也能通过。
乙:咱4人都不能过。
丙:李娜能过。
丁:我看有人能通过。
甲:李 → 刑
乙:所有都不
丙:李
丁:有的是
乙、丁为矛盾关系,必有一真一假
根据乙、丁:李、刑通过
事后证明,四人中只有一个人的猜测不对,则可推出以下哪项结论?( )
A.甲猜测错误,刑燕通过
B.乙猜测错误,李娜没通过
C.丙猜测错误,刑燕没通过
D.乙猜测错误,刑燕通过
【例9】县领导参加全县的计划生育工作会,临时被邀请上台讲话。由于事先没有做调查研究,也不熟悉县里计划生育的具体情况,只能说些模棱两可、无关痛痒的话。他讲道:“在我们县14个乡中,有的乡完成了计划生育指标;有的乡没有完成计划生育指标;李家集乡就没有完成嘛。”在领导讲话时,县计划生育委员会主任手里捏了一把汗,因为领导讲的三句话中有两句不符合实际。
①有的是
②有的不
③-李
①②为反对关系,必有一真
则③为假,李完成
根据:某个 → 有的
③为某个,则推出有的①
以下哪项正确表示了该县计划生育工作的实际情况?( )
A.在14个乡中至少有一个乡没有完成计划生育指标
B.在14个乡中除李家集乡外还有别的乡没有完成计划生育指标
C.在14个乡中所有的乡都完成了计划生育指标
D.在14个乡中只有一个乡没有完成计划生育指标
【例10】在决定孩子上什么课外班的问题上,四位老人发生争执。姥姥说:“学习钢琴比较好。”姥爷说:“如果学习视唱练耳,那么也应该学习钢琴。”奶奶说:“不应该学习钢琴,应该学习视唱练耳。”爷爷说:“不应该学习视唱练耳。”
①钢琴
②视唱 → 钢琴
③-钢琴 且 视唱
④-视唱
②③为矛盾关系,必有一真一假
则:①④为假
如果四人中只有一人是对的,那么可以推出( )。
A.不学钢琴,学习视唱练耳
B.既不学钢琴,也不学视唱练耳
C.学习钢琴,不学视唱练耳
D.既学钢琴,又学视唱练耳
【例11】今年春运对全市中巴客运车的安全检查后,甲、乙、丙三名交警有如下结论:
甲:所有中巴客运车都存在超载问题。
乙:所有中巴客运车都不存在超载问题。
丙:如意公司的中巴客运车和吉祥公司的中巴客运车都存在超载问题。
①所有都
②所有都不
③如意且吉祥
①②为反对关系,必有一假
则:③为真话
继续推理:则②为假,①为真
如果上述三个结论只有一个错误,则以下哪项一定为真?( )
A.如意公司的中巴客运车和吉祥公司的中巴客运车都不存在超载问题
B.如意公司的中巴客运车和吉祥公司的中巴客运车都存在超载问题
C.如意公司的中巴客运车存在超载问题,但吉祥公司的中巴客运车不存在超载问题
D.吉祥公司的中巴客运车存在超载问题,但如果公司的中巴客运车不存在超载问题
【例12】甲和乙都有可能受邀参加某专家论坛。现在,甲得知了以下消息:
(1)论坛主办方决定,至少邀请甲或乙中的一位;
(2)论坛主办方决定不邀请甲;
(3)论坛主办方一定会邀请甲;
(4)论坛主办方决定邀请乙。
①甲或乙
②-甲
③甲
④乙
②③为矛盾关系,必有一真一假
则:①④一真一假
若④为真,①为真
则:④为假,①为真
①或关系否一推一,邀请甲,不邀请乙
假如上述消息中,两条为真,两条为假,则( )。
A.论坛主办方决定邀请甲,不邀请乙
B.论坛主办方决定邀请乙,不邀请甲
C.论坛主办方决定同时邀请甲和乙
D.论坛主办方决定既不邀请甲,也不邀请乙