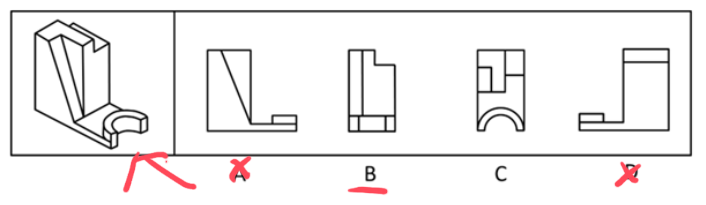
Appearance
空间重构
考点一:六面体
1.如果靠想象力:注意折叠方向
左边给定的是纸盒外表面的展开图,右边哪一项能由它折叠而成?

2.如果靠技巧:所有的方法都是排除错误选项的
如果选择A项,不需要知道为什么对,所有的方法和技巧都是排除错误选项,只需要知道3个选项错误,剩下的选项正确即可。
方法一:相对面
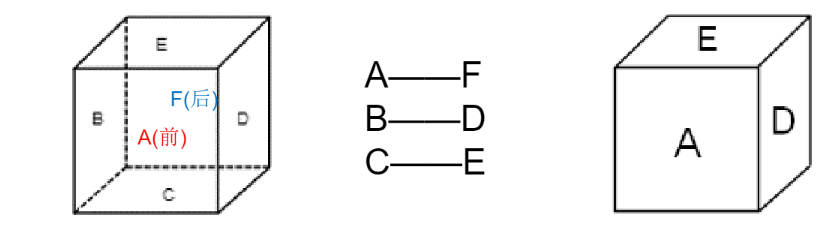
应用:一组相对面同时出现的选项——排除
展开图中如何判断相对面?
1.同行或同列相隔一个面
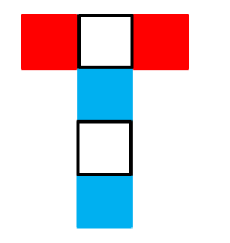
两个红色中间间隔一个白色,两个红色是相对面。两个白色中间间隔一个蓝色,两个白色是相对面。两个蓝色中间间隔一个白色,两个蓝色是相对面。
2.“Z”字形两端(紧邻“Z”字中线的面)
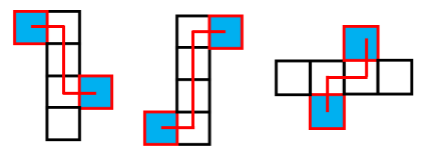
蓝色面在“Z”字中线两端,蓝色面是相对面。“Z”字有3条线,中间的线是中线,中间紧邻着的两端是相对面。
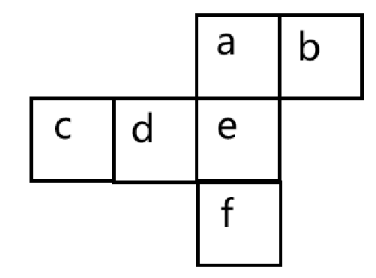
紧邻“Z”字中线的面,面b和面d是相对面。面a和面f中间间隔一个面,是相对面。面c和面e中间间隔一个面,是相对面。
【例1】(2021事业单位)下图是给定的纸盒的外表面,选项中哪一个是由此外表面折叠而成的纸盒?
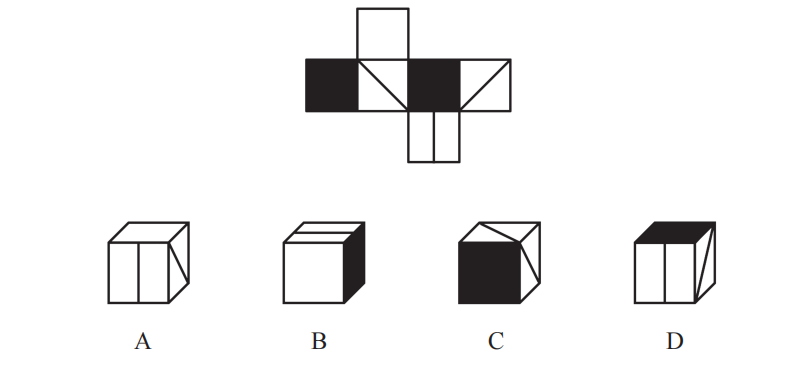
【解析】
1.先不找题干的相对面,可能不能用相对面做题,也可能会忘记谁和谁相对,做题首先看选项,先定位选项的面,然后看是否出现相对面。
A项:正面是竖线面,白色面对应对号面,如下图,两者是“Z”字两端的相对面,相对面不能同时出现,排除。
B项:该项的正面和顶面也是“Z”字两端的相对面,如下图,相对面不能同时出现,排除。
C项:正面是黑色面,不知道是题干哪个面,上面和右面对应题干2个斜线面,两个面是相对面,不能同时出现,排除。
A、B、C项均排除,D项当选。【选D】
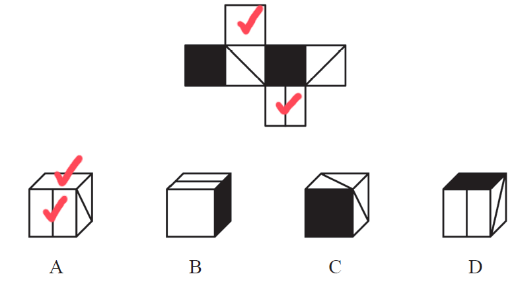
【例2】(2022天津)左边给定的是纸盒的外表面,右边哪项能由它折叠而成?
【解析】
2.标号1-6,标号只是为了方便讲解,自己做题可以不标号。
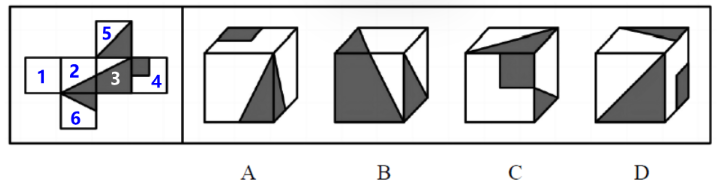
A项:正面和右侧面一个是面2、一个是面6,顶面是面4,面2和面4是中间间隔一个面的相对面,相对面不能同时出现,排除。
B项:正面是面3,右侧是面5,面5和面6是相对面,顶面不可能是6,顶面是2,没有涉及相对面,保留。
C项:正面是面4,顶面是面5,右侧不能是面2,因为面2和面4是相对面,也不能是面6,因为面5和面6是相对面,排除。
D项:正面是5,右侧是面4,上面不能是面2,因为面2和面4是相对面,也不能是面6,因为面5和面6是相对面,排除。【选B】
方法二:相邻面——公共边
如何确定公共边:
1.平面图中构成直角的两条边是同一条边

面A的右侧边、面C的上边构成直角边,两条边是同一条边。
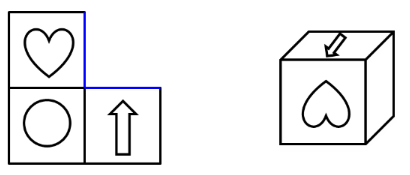
箭头和心形有公共边,在展开图中和立体图中找到公共边,立体图中心的“尖”对着公共边,展开图心的侧面对着公共边,而不是“尖”对着公共边,对应不一致。
2.一列/行连着4个面,两头的两条边是同一条边
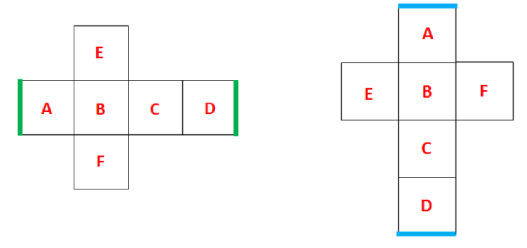
图1的A、B、C、D这4个面连在一起,面E是“盖”,面F是“底”,面A、B、C、D可以围成一圈,左右两头的两条边是同一条边。可以将面A移动到面D右边,原来A的左侧是公共边,移动过来之后没有任何变化,A的左侧是公共边,4个面连在一起,左边的面可以移动到右边,右边的面可以移动到左边。图2的A、B、C、D这4个面连在一列,上下蓝色边是公共边,一列4个面同理,上面的面A可以移动到面D下面,下面的面D可以移动到面A上面。
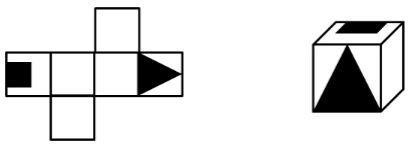
展开图中4个面连在一起,最左侧和最右侧是公共边,展开图中公共边挨着黑方块,立体图中公共边没有挨着黑方块,对应不一致。
3.“3+1构成L形”,同方向的两条边是同一条边
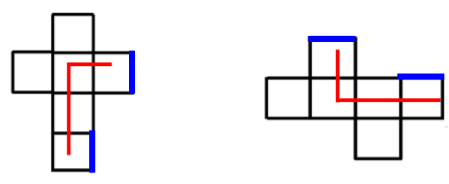
图2上面1个面和下面3个面构成L型,短边指着的边和另一侧上边是公共边。可以记忆为直角边是公共边,往左、往右延伸一次之后依然是公共边。“L”型像是一个人在坐着,头和脚就是公共边。

涉及面F、T、V这3个面,构成“3+1”“L”型,红边是公共边,立体图“V”的尖对着公共边,展开图中“V”的开口对着公共边,对应错误。
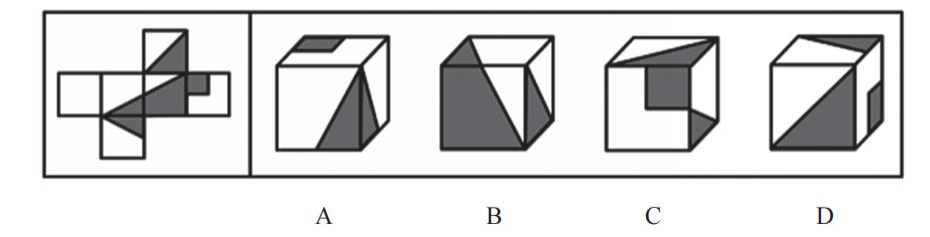
【例3】(2023江苏)左边给定的是一个六面体的外表面展开图,右边哪一项能由它折叠而成?
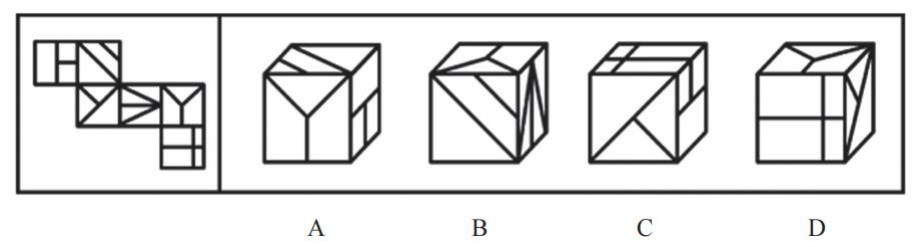
【解析】3.标号1-6,对应选项的面。
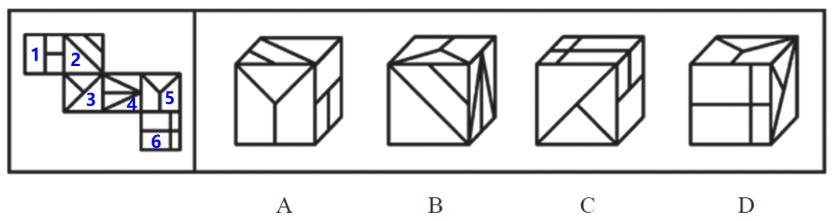
A项:正面是面5,顶面是面2,右侧是面1,面1和面2挨着有公共边,该项的“T”方向反了,该项是面1大长方形挨着公共边,展开图是面1中2个小正方形挨着公共边,排除。
B项:正面是面2,顶面是面5,右侧是面4,面2和面4的公共边没有问题,面5和面4的公共边没有问题,面5和面2是“L”型,可以看公共边,没有问题,不建议直接选择该项,考试时很紧张,可能会犯错,建议看完剩余选项,保留。
C项:正面是面3,顶面是面6,右侧是面1,该项面3的长斜线和面1的小竖线挨得很近,立体图中面3的长斜线和面1的小竖线并没有挨着很近;该项面1的“T”字左边是正面(面3),展开图中面1的“T”字右边是面3;还可以看面1和面6的公共边,该项面1的2个正方形挨着面6的长方形,展开图中面1的正方形挨着面2,面6长方形挨着面4,对应不一致,排除。
D项:正面是面6,顶面是面5,右侧是面3,面5和面3是相对面,相对面不能同时出现;面3和面6是“L”型,该项公共边挨着小三角形,展开图公共边挨着大三角形,排除。
答疑:六面体中两个面不是相对面就一定有公共边。【选B】
【例4】(2024江苏)左边给定的是六面体的外表面展开图,右边哪一项能由它折叠而成?
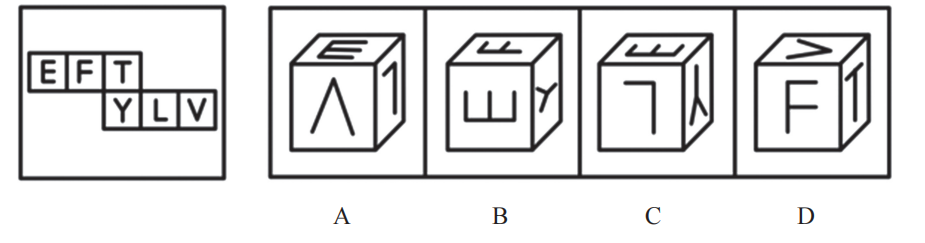
【解析】4.看选项定位面。
A项:展开图中面“E”的开口对着“F”,该项“E”的开口对着“L”,对应不一致,排除。
B项:展开图中“Y”的开口指着“T”,该项“Y”的开口指着“E”,排除。
C项:“Y”和“L”没有问题,“E”和“Y”是“L”型,展开图“Y”的尖指着“E”,该项也是“Y”的尖指着“E”,没问题,保留。
D项:“L”型的头和脚是公共边,展开图“V”的开口对着“T”,该项是“V”的尖对着“T”,排除。【选C】
【例5】(2024国考)左图为8个白色正方体和4个灰色正方体粘接而成的长方体,右边哪一个可能是其外表面展开图?
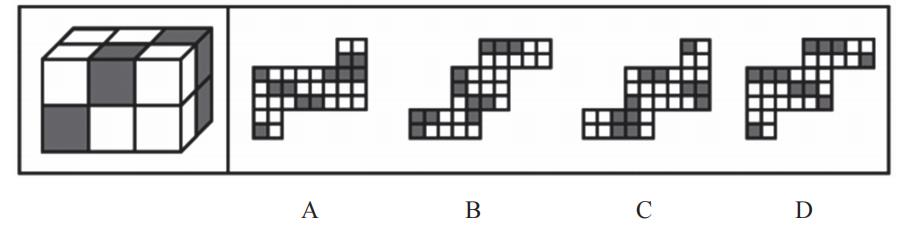
【解析】5.本题比较难,正确率在30%~40%。本题和前面的题不一样,是小正方体组成,类似魔方。题干说明8个白色正方体和4个灰色正方体,4个灰色正方体都可以看到,看不到的是白色块。
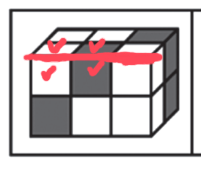
公共边等长且同色,如下图一,红色的公共边,两侧的颜色一定相同,因为小立方体是个整体,公共边一定等长且相同颜色,只需要找直角边的公共边,如下图二。
A项:画出直角边的公共边,2个白色挨着1白1灰,排除。
B项:直角边没问题,保留。
C项:直角边没问题,保留。
D项:直角边没问题,保留。
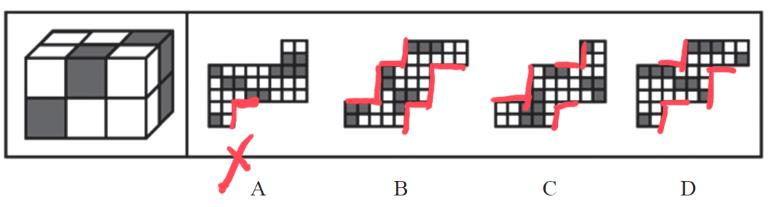
接下来看每个面中的灰块数量不能出错,每个面中的灰色块是确定的,正面有2个灰色,顶面是2个灰色,右侧面是2个灰色,下面是2个灰色,左侧面是1个灰色,后面是2个灰色,1个面中不能出现3个灰色,分割选项中的面。
B项:如下图三,红色直角边是公共边,公共边等长,则左下是个长方形,紧挨着右侧也是长方形,直角边是公共边,右上也是长方形,左上是正方形,蓝色对号面是3个灰块,排除。
C项:如下图三,直角边是公共边,分割面,左下是长方形,蓝色对号面是3个灰块,排除。A、B、C项均排除,D项当选。
D项:直角边是公共边,左下是正方形,中间都是长方形,右上是长方形,没有涉及3个灰块的面,考试时不需要看该项,排除3个选项就可以选择该项,当选。【选D】
图一
图二
图三
【注意】
1.公共边等长且同色。
2.每个面中的灰块数量不能错。
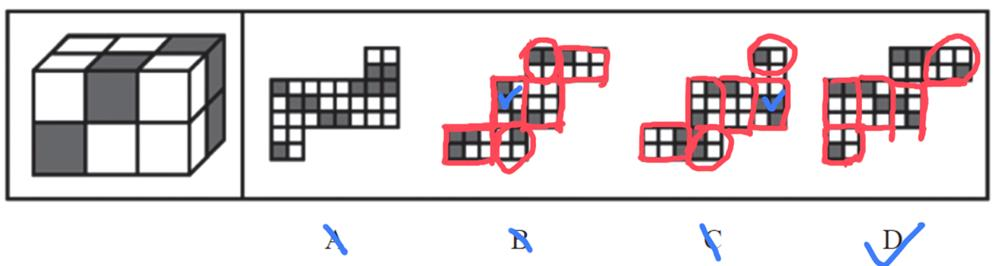
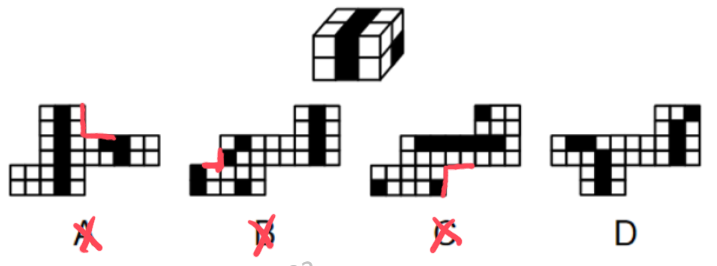
练一练(2025国考)下图为4个黑色、8个白色正方体粘接成的长方体,问哪一项可能是其正确的外表面展开图?
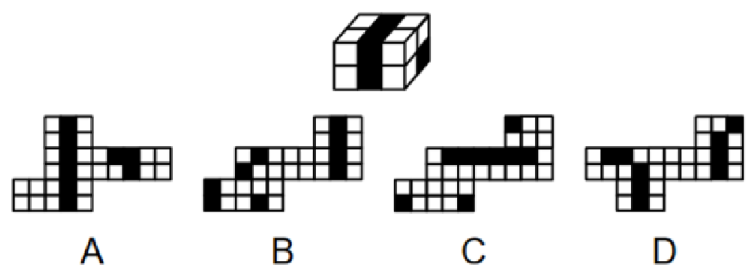
【解析】拓展.找公共边颜色相同,如下图。
A项:2个白色挨着1白1黑,排除。
B项:红色直角边是白色和黑色挨着,排除。
C项:直角边是2个白色挨着1白1黑,排除。
A、B、C项均排除,D项当选。
答疑:关于面的分割问题。利用直角边,直角边是公共边,直角边是2个方块就是正方形,3个方块就是长方形。【选D】
方法三:相邻面——公共点
如何确定公共点: 相邻三个面的公共点是唯一的
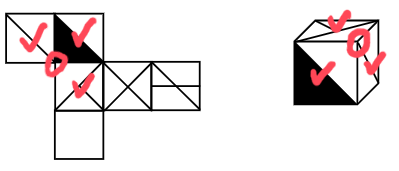
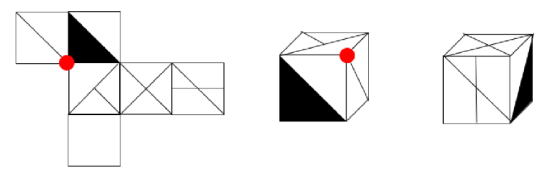
立体图的公共点是圈出的点,在展开图中找到对应的面,圈出的点是公共点,展开图公共点挨着黑色三角形,立体图公共点没有挨着黑色三角形,对应不一致。
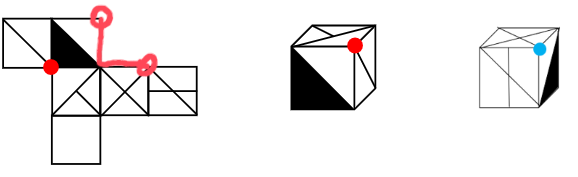
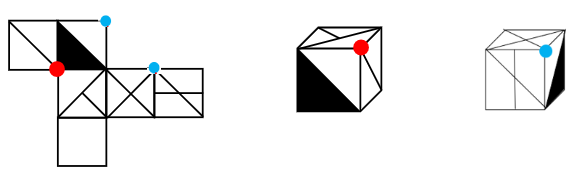
蓝色点是公共点,在展开图中找到对应的面,借助直角边找公共点,红色直角边是公共边,红色边会重合,画圈的2个点是同一个点,蓝点是公共点,展开图公共点引出2条线,立体图中公共点引出1条线,对应不一致。
三个面挨在一起——优先公共点
三个面没有挨在一起——优先公共边
用公共点还是公共边没有绝对的优先级,有时用公共边,有时用公共点,有时公共边或者公共点都可以。3个面挨着,公共点好找可以看公共点,若3个面没有挨在一起,优先公共边。
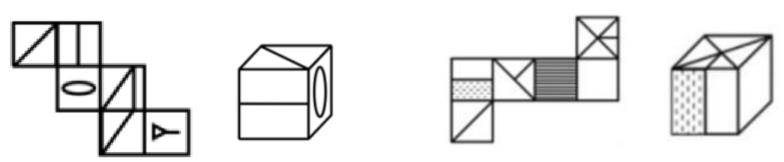
1.如图一,3个面挨在一起,公共点很好找,展开图中公共点没有引出线,立体图中公共点引出1条线,对应错误。
2.如图二,3个面离得比较远,不好找公共点,看公共边,4个面连在一起,最左侧和最右侧是公共边,立体图公共边挨着全白,展开图中挨着一半白、一半阴影,对应错误。
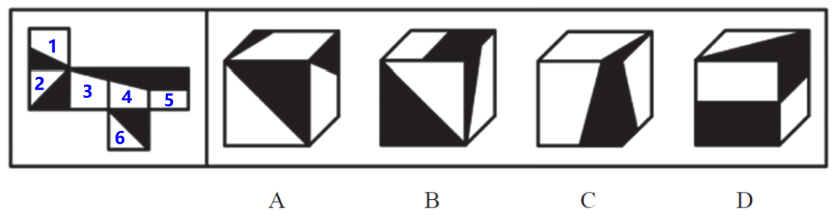
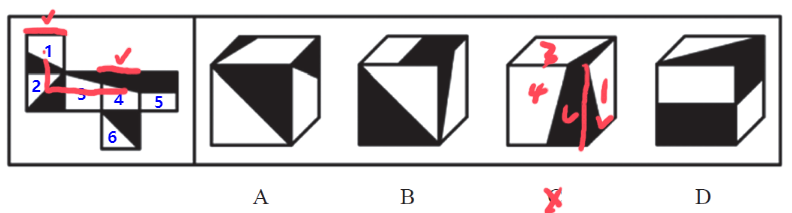
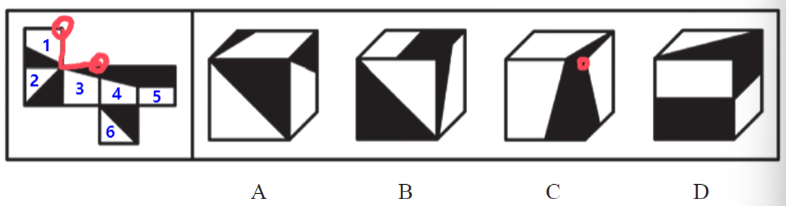
【例6】(2024浙江选调)左边给定的是纸盒的外表面,右边哪项能够由它折叠而成?
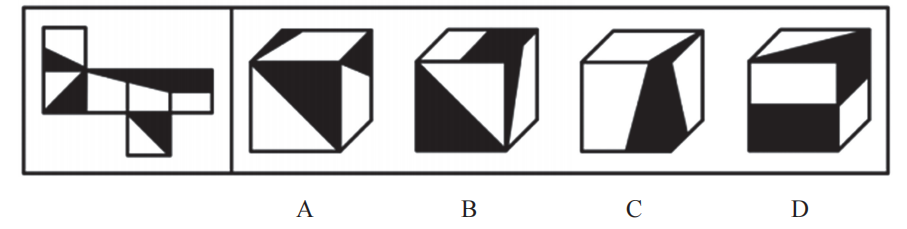
【解析】6.标号1-6,面1和面3不一样,面1在中点,面3在三分之一处,三角面积更小一些,看选项定位面。
A项:正面是面2或者面6,顶面是面3,右侧是面1,有面1不能有面6,属于“Z”字两端的相对面,则正面是面2,3个面挨着,观察公共点,该项公共点挨着面1和面2的黑色,展开图公共点挨着3个面的黑色;也可以看面1和面 3的公共边,直角边是公共边,该项公共边挨着面3白色,展开图中公共边挨着面3的黑色,排除。
B项:正面是面2或者面6,先看知道的面,顶面是面5,右侧是面1,有面1不能有面6,“Z”字两端的相对面,则正面是面2,面1和面2的公共边没有问题,面2和面5是4个面连在一起,两头是公共边,也没有问题,面1和面5不好观察,保留。
C项:正面是面4,顶面是面3,右侧是面1,“L”型,如下图二,头和脚是公共边,该项是黑色和黑色挨着,展开图是面4的黑色挨着面1的白色;也可以看公共点,如下图三,直角边是公共边,画圈的点是公共点,展开图公共点只挨着面3和面4的黑色,没有挨着面1的黑色,该项公共点挨着3个面的黑色,排除。
D项:原图中只有一个面5,该项出现2次,其中一个是无中生有的面,排除。【选B】
图一
图二
图三
【例7】(2024联考)右边哪项不能由左侧展开图折叠而成?
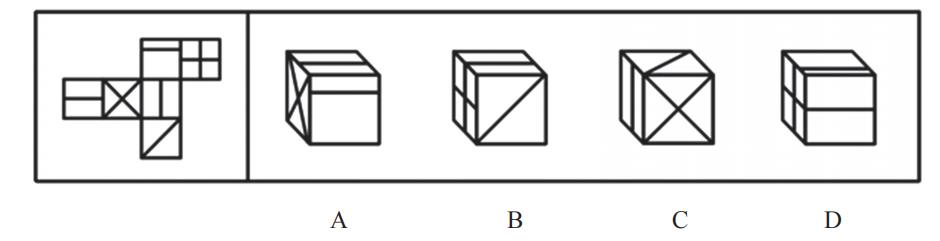
【解析】7.本题比较难。首先看问法,问“哪项不能由左侧展开图折叠而成”,找错误的选项。面3和面5长得一样,需要判断是哪个面。
A项:正面是面1,左侧是面4,展开图中面3的线垂直面4的公共边,面5的线平行公共边,该项顶面的线垂直面4的公共边,则该项顶面是面3,没看出问题,排除。
B项:正面是面6,左侧是面2,该项面2和顶面的线连在一起,展开图面2和面5的线没有连在一起,则顶面是面3,面3和面6的公共边看不出问题,面2和面6的公共边看不出问题,排除。
C项:正面是面4,上面是6,左侧面和面4公共边平行,展开图面3和面4公共边垂直,则左侧不能是面3;如果左侧是面5,3个面挨在一起有公共点,该项公共点引出面6的斜线,展开图中公共点没有引出面6的斜线,该项不可能,考试直接选择该项,当选。
D项:顶面是面1,左侧是面2,正面不是面5,因为展开图面5的线和面1垂直,而该项平行,考虑正面是面3,面1和面3构成“L”型头和脚是公共边,面3的线和公共边平行,该项没有问题,排除。【选C】
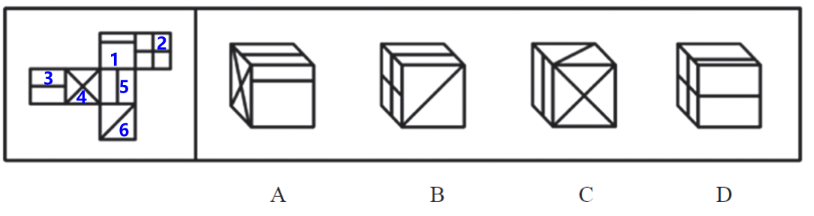
方法二:相邻面——画边法
①结合选项,找一个特殊面的唯一点或唯一边
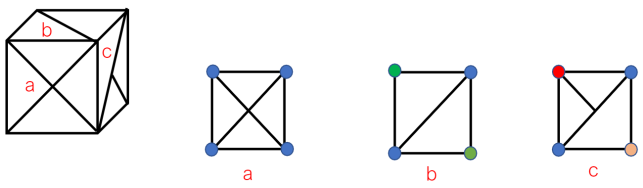
图一
如图一,一个面有4个顶点,如果有一个顶点和其他顶点长得不一样,则是唯一点。
图一中,图a的4个蓝色点长得都一样,没法区分谁是谁,没有唯一点;图b中两个蓝色点没法区分,两个绿色点没法区分,都不是唯一点;图c中两个蓝色点不好区分,但红色点和其他点不一样,红色点只引出一条小短线,两个蓝色点引出长对角线,红色点是唯一点。除此之外橘色点也是唯一点,因为橘色点没有引出线条。
②顺/逆时针方向描边标号(描同一个面)
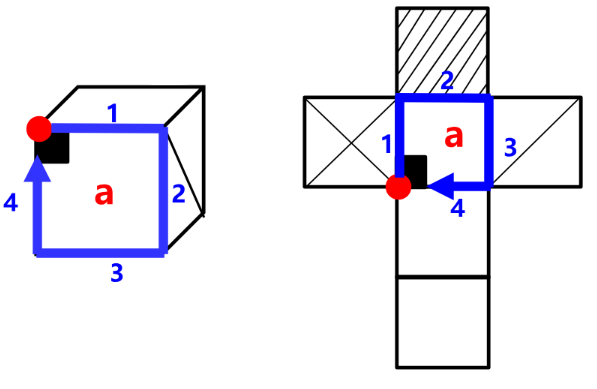
图二
如图二,立体图形中黑色方块挨着的点是唯一点,在展开图中也可以找到相同面上相同的黑色方块挨着的点,把面a看成一个“操场”,顺时针跑一遍,跑的第一条边是边1,顺时针下一条边是边2,依此类推,标记边1~4。
③题干与选项对应面不一致——排除
如图二,立体图形边1对应白色面,展开图中边1对应“×”面,对应不一致,可以排除选项。
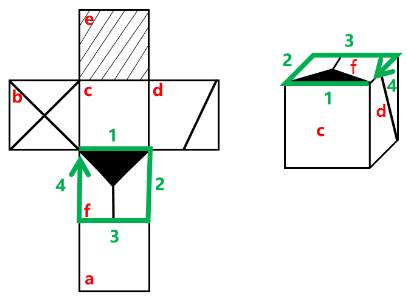
图三
唯一边:除了唯一点也可以找唯一边。如图三,面f中没有唯一点,但有唯一边,只有一条边是纯黑色的,标记为边1,沿着顺时针标记边1~边4,在展开图和立体图形中都标记边1~边4。展开图和立体图形中边1都标记空白面,但展开图中边4标记面b,立体图形中边4标记面d,对应不一致。
【例8】(2024四川)左图是给定纸盒的外表面,右边哪项能由它折叠而成?
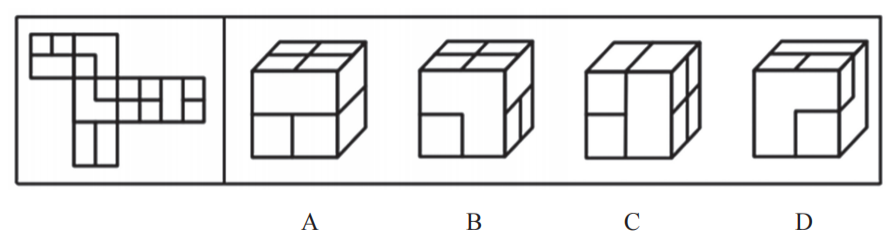
【解析】8.本题较难,难点在于展开图中面a和面e长得一样,面b和面c长得也是一样的。可以先尝试公共边、公共点的方法能不能解题。
A项:上面为面d,右面为面f,立体图形已经有面d则正面不能是面a,因为展开图中面a和面d是相对面,则正面只能是面e。根据公共边、公共点看不出问题,先放着。
B项:上面为面d,右面为面e(面a和面d是相对面,则能是面a),正面为面b(面e和面c是相对面),看不出问题,先放着。
C项:上面一定是面f,右面一定是面d,则正面不能是面a,只能是面e,看不出问题,先保留。
D项:正面、右面可能是面b或面c,则上面只能是面a(面c和面e是相对面),展开图中三个面紧密相连,直接看公共点,展开图中公共点挨着面a的大长方形,选项中公共点挨着面a的小正方形,对应不一致,排除。
看公共边和公共点选不出答案,考虑画边法,A、B、C项都出现了面e,根据面e画边就可以判断3个选项。面e没有唯一点,但有唯一边,有一条边没有挨着内部的“T”字,这个边是特殊边,把这个边标记为边1,在展开图中和A、B、C项中从同一条边1按照顺时针画边标记为1~4。
A项:展开图和选项的边1挨着“十”字面,没有问题;展开图中边2挨着面b,选项中边2挨着面f,对应不一致,排除。
B项:展开图中边4挨着面f,选项中边4挨着面b或者面c,对应不一致,排除。
A、B、D项均排除,C项当选。【选C】
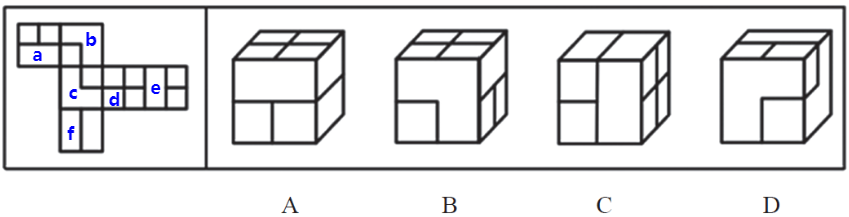
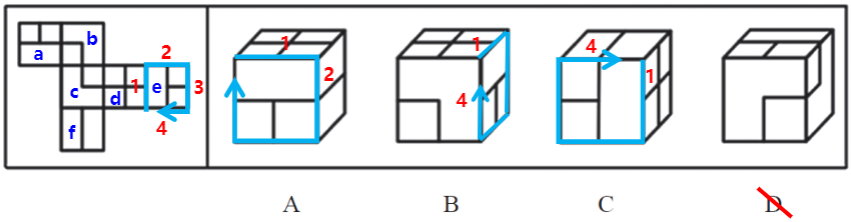
【例9】(2022国考)下列纸盒的外表面展开图中,哪项折叠成的纸盒和其他三个不一样?

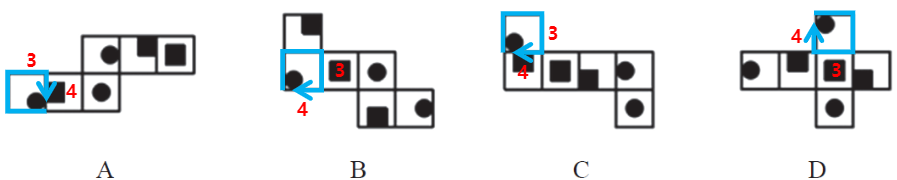
【解析】9.问“哪项折叠成的纸盒和其他三个不一样”,遇到这种问法的题目,统一用画边法,有时候公共边或者公共点没法解题,但画边法一定可以解题。在展开图中找有唯一点或者唯一边的面,只有面3和面6没有,其他几个面都有唯一点或者唯一边。这种题目有出题的套路,90%的题目中都可以用A项最左侧的面画边来解题。在A项中最左侧的面中,黑球挨着的顶点是唯一点,按照顺时针标记为边1~边4,在其他选项中也按同样的方式标记边。这里A项中边1挨着的面不知道是谁,边2挨着的面也不知道是谁,则只要知道边3和边4挨着的面是谁即可。
A项:边3有“3+1”的“L”型的公共边,则边3挨着黑色小球面。
B项:边3挨着黑色方块面。
C项:边3挨着黑色方块面。 此时B、C项边3挨着的面是一样的,A项和B、C项不一样,则直接选择A项即可。验证D项(考试的时候不需要验证),D项的边3也是挨着黑色方块面,没有问题,A项当选。【选A】
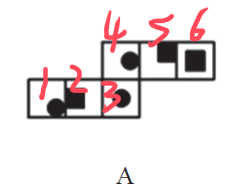
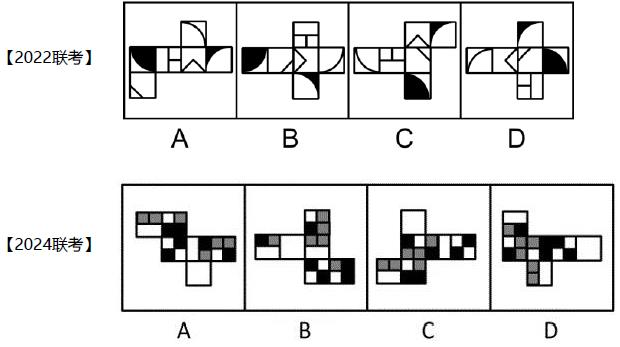
画边:
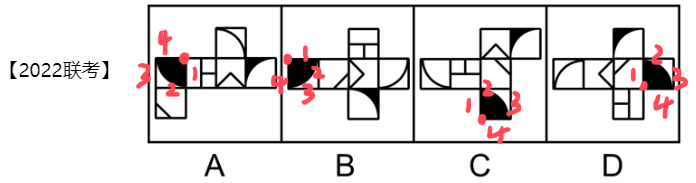
如果A项最左边有两个面,就找左上方的面。以扇形的直角顶点为唯一点,在四个选项中按照顺时针标记为边1~边4,A项的边1挨着“T”字,B项的边1挨着“T”字,C项的边1挨着“T”字,D项的边1挨着三角形面,D项和其他选项不一致。
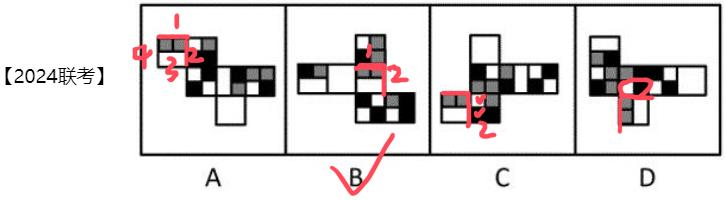
在A项最左边的面画边,以纯黑色的边为边1,顺时针画边标号,在四个选项中标记出边1~边4,A项的边1看不出挨着谁,但边2挨着一白一黑,B项的边2挨着一黑一灰,C项的边2挨着一白一黑,D项的边2挨着1白一黑,B项和其他选项不同。
技巧:如果A项最左边只有一个面,就用这个面画边;如果A项最左边有2个面,就用左上方的面画边。
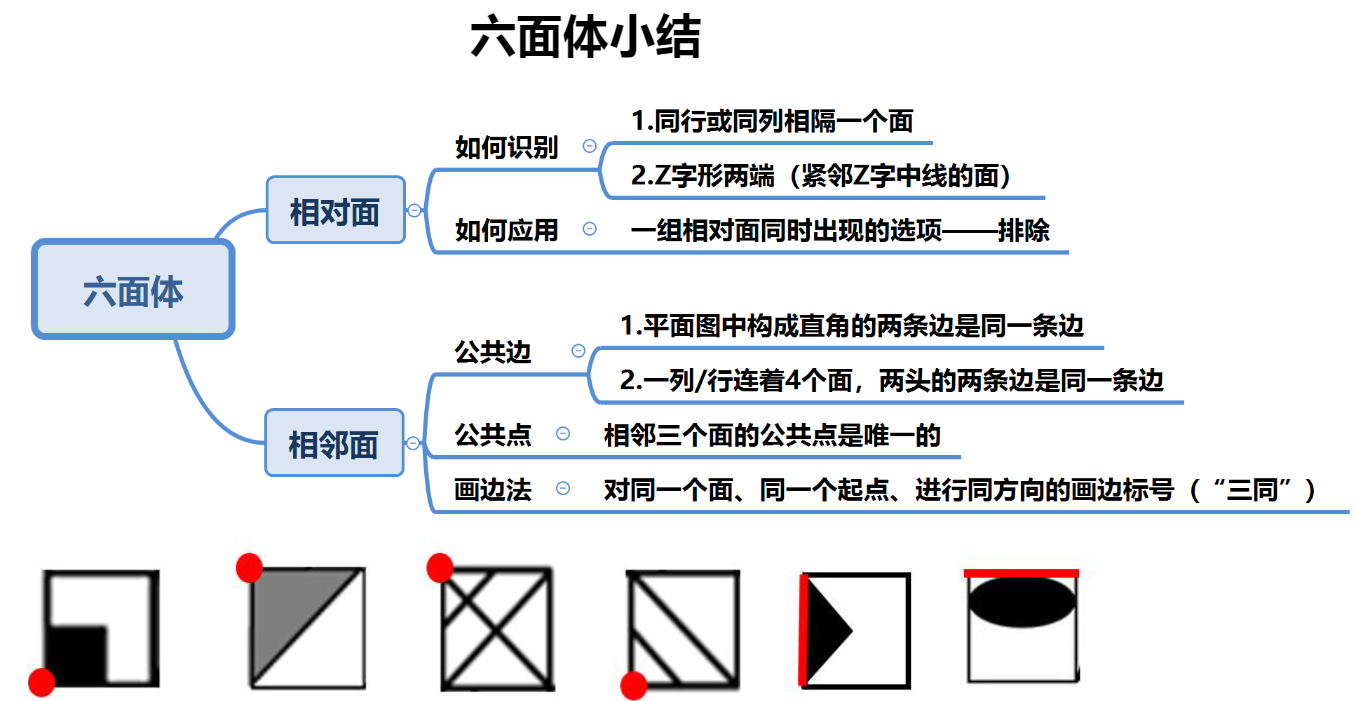
考点二、截面图
截面图——指的是被切部分的形状
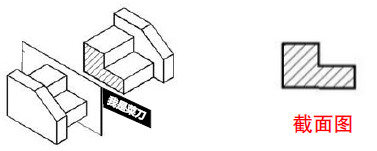
注意截面图是指被切的部分紧紧挨着刀面的部分,如图中只有阴影部分是截面。
常见立体图形截面(以最常见的六面体、圆柱、圆锥、圆台等基础图形为例)
1.正方体/长方体
(1)矩形(拦腰切、上下切、斜切)
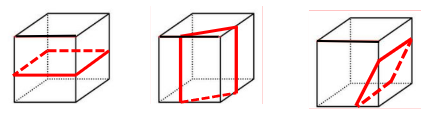
(2)梯形(斜切)
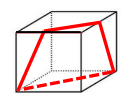
(3)三角形(从棱上的某一点开始斜着切到面)
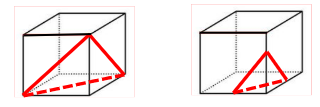
PS:
长方体/正方体只能切出锐角三角形,切不出直角三角形和钝角三角形,这里可以用余弦定理证明,但做题不需要知道如何证明,知道结论即可。
梯形斜切,切不出直角梯形,能切出两边都是直的,但切不出来一边是直的。
2.圆柱
(1)圆(横切)(2)椭圆(斜切)(3)矩形(竖切)

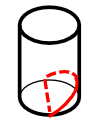
注意:圆柱斜切,切不出梯形
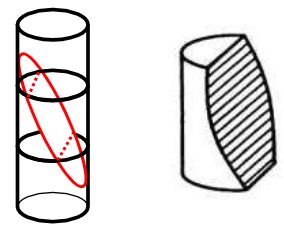
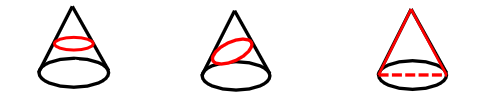
3.圆锥
(1)圆(横切)(2)椭圆(斜切)(3)三角形(竖切)
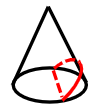
4.圆台
(1)圆(横切)(2)椭圆(斜切)(3)梯形(竖切)
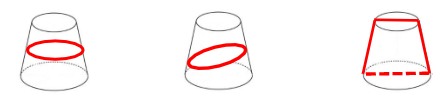
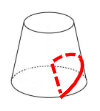
如果三种图形从侧面斜切到底面,切出的是“D”形(半圆弧+直线),这里的弧一定是椭圆的弧,一般不会在这里设坑,因为椭圆的弧会无限接近于半圆弧。
截面图中常挖的“坑”
(1)正六面体,不能切直角三角形、钝角三角形、直角梯形
(2)圆柱,不能切出梯形
【哪项不可能】
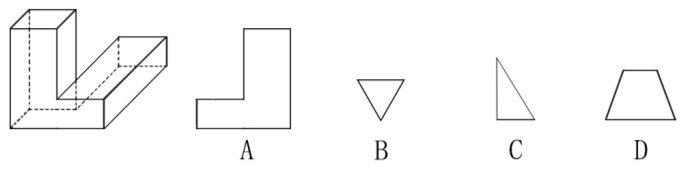
如图,题干可以拆分成两个六面体,六面体切不出直角三角形,可以直接选择C项;A项从原图的正面或者下面可以直接看到,能看到就可以切出;长方体也可以切出锐角三角形和梯形,排除B、D项。
【例1】(2021广东)下图所示立体图形沿OMN面斜切,由切面所见截面最可能是:
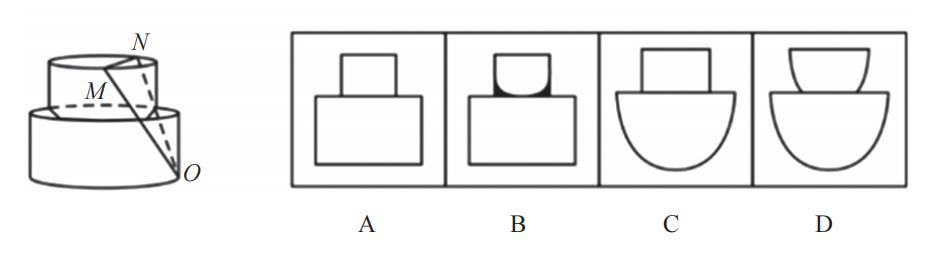
【解析】1.图形上下是圆柱,斜切的时候两侧一定是弧线,只有D项符合,D项当选。【选D】
【例2】(2020国考)左图为给定的立体图形,将其从任一面剖开,右边哪项不可能是该立体图形的截面?
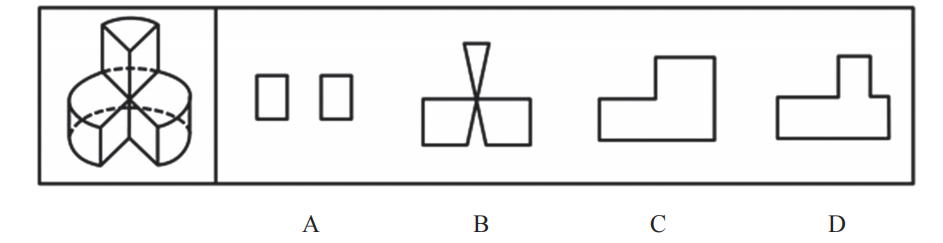
【解析】2.上方和下方都是圆柱少了一部分,都相当于圆柱,问“不可能的截面”,选非题。
A项:直接经过下方竖切可以切出,排除。
B项:上方往下斜着切可以切出三角形,继续斜切,刀经过下方的圆柱,两侧一定是弧线,不能是直线,切不出来,当选。
C项:从上到下竖切可以切出,排除。
D项:竖切可以切出,上方的矩形调整角度就可以得到,排除。【选B】
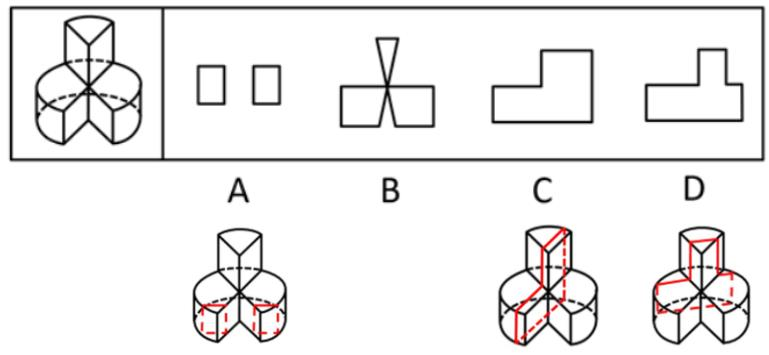
(3)当图形中挖空了一个小图形时,注意“空心”没有实线
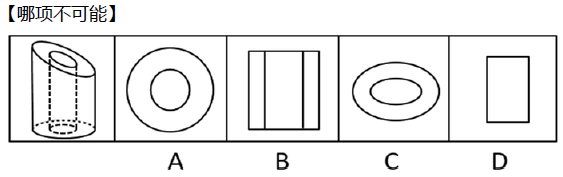
4.例:问哪项不可能切出。A项有两个圆,横切即可;B项要得到长方形需要竖着切,但立体图形中间是空的,竖着切不能有线,当选;C项斜着切即可;D项不经过空心的地方竖着切即可。
(4)复杂图形做拆分,不同角度,不能共存
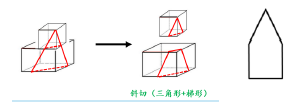
如图,立体图形可以拆分为上下两个六面体,截面也可以拆分成上方三角形、下方矩形。上方要切出三角形需要斜着切,斜着切刀下面,切不出梯形,因为下方要切出梯形需要竖着切,但刀不能拐弯,切不出来。
【例3】(2019四川下)左图给定的是由4个相同正方体组合成的立体图形,将其从任一面剖开,右边哪一项不可能是该立体图形的截面?
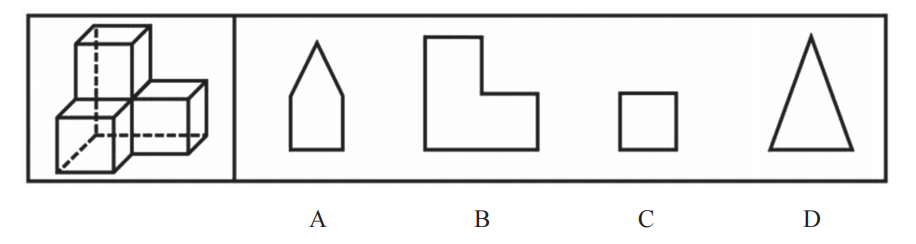
【解析】3.立体图形是4个正方体组成的,问“不可能的截面”,选非题。如果不知道怎么做,可以排除法解题。
B项:从左边、右边、下面都能看到,能看到就一定可以切出,排除。
C项:一定可以切出正方形,竖着切一刀即可,排除。
D项:锐角三角形一定可以切出,排除。
综上,B、C、D项均排除,A项当选。
A项:上方斜着切可以切出三角形,但下方的矩形必须直着切,而刀不能拐弯,切不出来,A项当选。【选A】
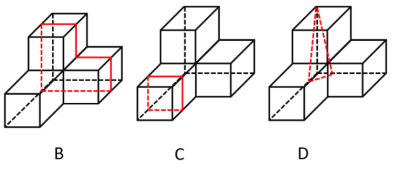
【例4】(2025国考)左边为给定的多面体,现用经P、Q、R三个顶点的平面对其进行切割,则哪个选项是其切面?
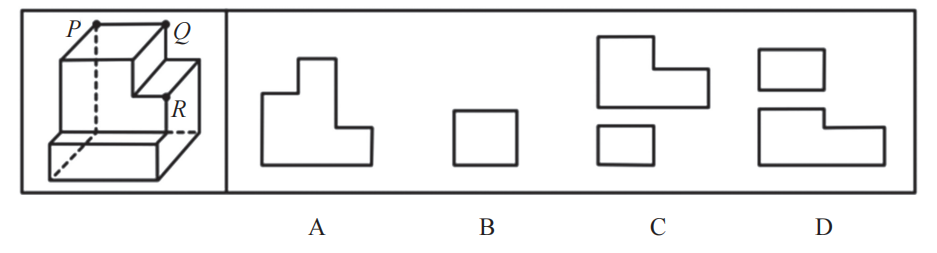
【解析】4.属于创新考法,经P、Q、R三个顶点的平面对其进行切割,问哪 个选项是切面。根据高中知识,三个点一定能构成一个唯一的平面,要把这个面画出来,第一件事是连接两个点,让这条线在立体图形的表面,先连接PQ。过点R做PQ这条直线的平行线,因为两条平行线可以确定唯一一个平面,这样就可以得到下刀和出刀的两条线,这样切出来的是一个长方形,B项当选。【选B】
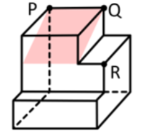
【注意】解题步骤:
1.连接两个点,让两个点的连线在立体图形的表面。
2.过第三个点做连线的平行线。
练一练(2025国考)左边为给定的多面体,现用经P、Q、R三点的平面对其进行切割,问哪个选项是其切面?
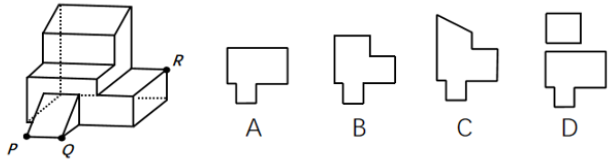
2.过第三个点做连线的平行线。 练一练(2025国考)左边为给定的多面体,现用经P、Q、R三点的平面对其进行切割,问哪个选项是其切面?
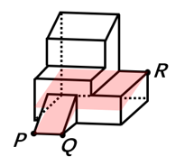
【例5】(2024国考)左图为13个白色正方体和5个灰色正方体组合而成 的多面体,现用经A、B、C三个顶点的平面对该多面体进行切割,正确的截面是:
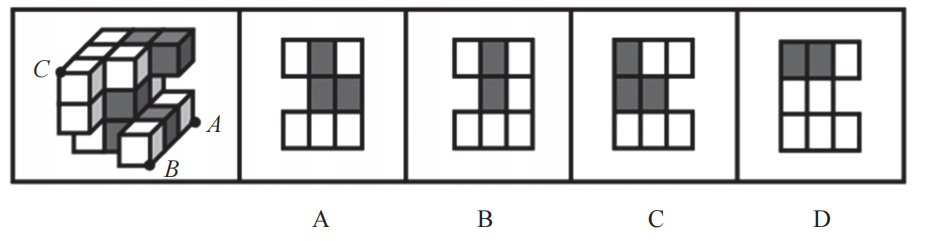
【解析】5.本题稍难,同样经过3个点切,连接AB,连线AB在立体图形表面,过C做AB的平行线,连接之后是斜切的。题干中5个灰色方块都在表面上,则看不到的地方一定是白色的。
切的时候是沿着对角线切的,如图,红色箭头指着的一行可以切到,蓝色箭 头指着的一行可以切到,粉色箭头指着的一行可以切到。红色的箭头切到了3个白色,蓝色的箭头切到了空、灰色、白色,粉色的箭头切到了白色、灰色、白色,画出对应的图形,注意观察的方向可以旋转,B项当选。
也可以不画,红色的箭头会切到0个灰块,蓝色的箭头只能切到1个灰块,粉色的箭头只能切到1个灰块,A项有3个灰块,C项有3个灰块,排除A、C项。B、D项的区别在于中间,B项中间是灰色,D项中间是白色,立体图形中间是灰色,B项当选。
这种题目一定是按照对角线切的,因为选项是长方形方块,横着切、竖着切都是正方形,只有斜着切是长方形;斜着切的时候,如果不按照对角线切,竖着的三个方块的边长不是一样长的,只有按照对角线切的时候才是一样长。【选B】
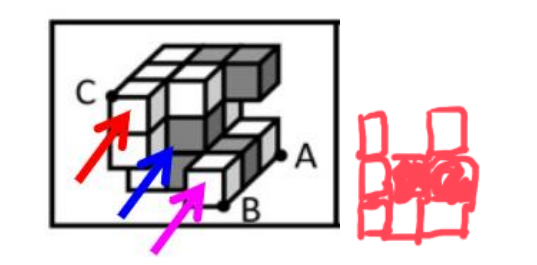
【拓展】(2024联考)下图为15个白色和5个灰色正方体组合而成的多面体,将其经A、B、C三个顶点切开后,正确的截面是:
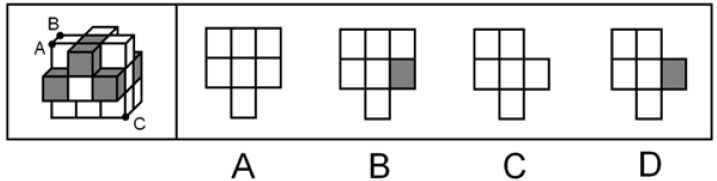
【解析】拓展.连接AB,过C做AB的平行线,沿对角线切,用三个箭头表示,红色箭头经过0个灰色,蓝色箭头经过0个灰色,粉色箭头经过0个灰色,一个灰色块都没有切到,排除B、D项。
比较A、C项,A项有2个空,C项有3个空,红色箭头会切到2个空,粉色箭头会切到1个空,一共会切到3个空,C项当选。【选C】
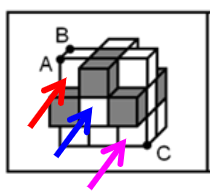
考点三:三视图
考查立体图形的多个观察角度:
主视图(从正面看)
左视图(从左侧看)
俯视图(从上向下看)
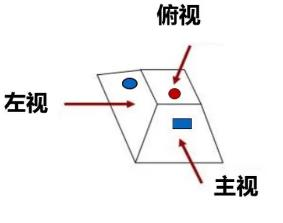
三视图
(1)观察到的视图都是平面图
(2)原图有线就有线,原图没线就没线
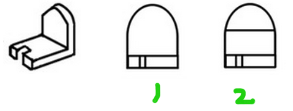
图一
(3)当被遮挡住时,看不见被遮挡部分
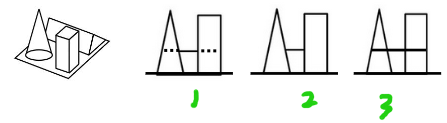
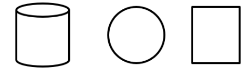
(4)某些角度下弧或斜线会被压平
【例1】(2021国考)左图为给定的多面体,从任一角度观看,右边哪项可能是该多面体的视图?
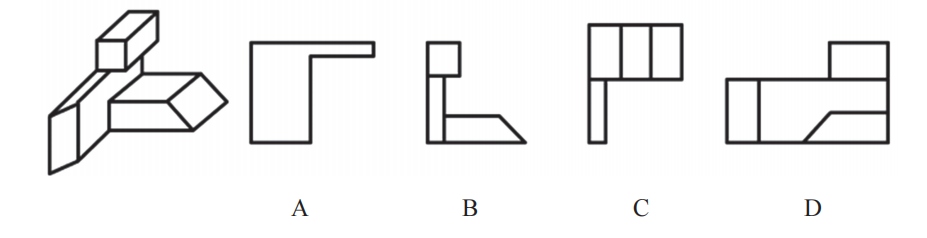
【解析】1.如果不看内部、只看外轮廓,立体图形从左或者从右边看的轮廓都是相同的,只是内部不同,所以观察选项的时候遇到轮廓相同的可以一起观察。如选项中A、C项的轮廓是相同的,只是相对着的角度,可以一起观察。
A、C项:A项是从下面看,但“刀把”的地方应该是斜着的,不是直角的,C项同理,均排除。
B项:从正面看可以得到,没有问题,当选。
D项:上方的长方形是从侧面看的,原图中下方左右两边的直线应该是平行的,但选项中下方是斜线,选项错误,排除。【选B】
【例2】(2024江苏)左图是由14个黑白小正方体组成的立体图形,右面四个选项中有一项不是该立体图形的视图,请把它找出来。
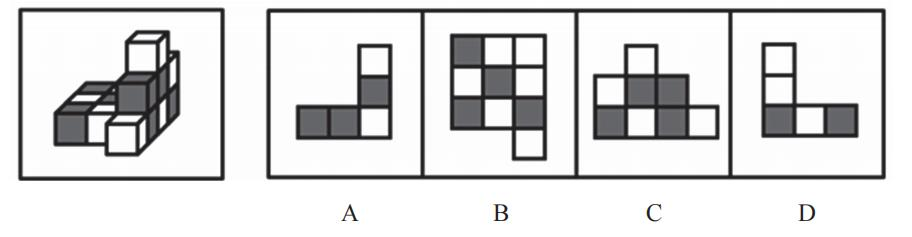
【解析】2.问“不是……的视图”,选非题。A、D项的轮廓相同,只是相对的角度,二者一起观察。从正面可以看到“L”型,可以看到2个灰块,但不是A项也不是D项;从后面看,最下方的两个是灰色的,D项有2个灰色,说明D项是从后面看的,则A项是不可能的,因为A项的轮廓要么是从正面、要么从后面看,但A项从正面和后面均不可能,则A项当选。
B项:从上往下俯视看,可以看到4个灰块,位置也没有问题,排除。
C项:从右边看不行,因为从右边看的话,最下方凸出的白色块应该在左边,
则选项是从左边看的,可以看到4个灰色,位置也没有问题,排除。【选A】
测验1.左边给定的是正方体的外表面展开图,下面哪一项能由它折叠而成?
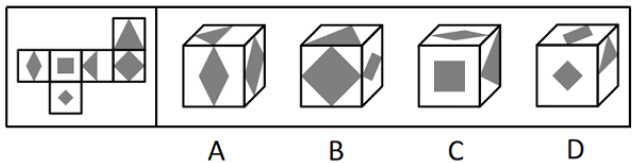
【解析】拓展1.对应面找关系。 A项:正面和顶面在展开图中是相对面,相对面不能同时出现,排除。
B项:正面和右面在展开图中有公共边(一行四个面两头的两条边),展开图中两个灰色方块没有挨着,选项中两个灰色方块挨在一起,对应不一致,排除。
C项:相邻面看不出问题,先放着。
D项:右面和顶面在展开图中是相对面,相对面不能同时出现,排除。
A、B、D项均排除,C项当选。【选C】
测验2.从一个圆柱体中挖去一个圆柱体和一个圆锥体,得到的立体图形如左图所示。则右边不可能是它的截面的是:
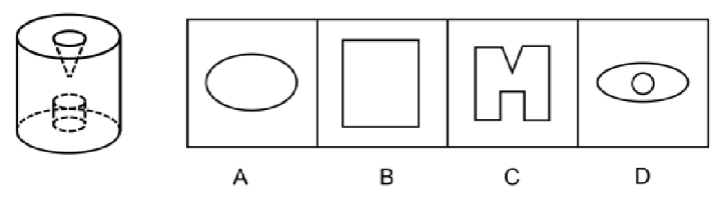
【解析】拓展2.课堂正确率为61%,易错C项。问“不可能”,圆柱斜切不切到空心就可以得到椭圆,A项排除。
圆柱从上到下竖着切,不切到空心就可以切出长方形,排除B项。
C项上面是倒三角形、下面是长方形,竖切可以切出,排除C项。
D项外面是个椭圆,内部是圆,横切得到圆,斜切得到椭圆,不同的角度不能共存,不能拐弯,D项当选。【选D】
测验3.左边为给定的立体图形,从任一角度观看,下面哪项不是该多面体的视图?
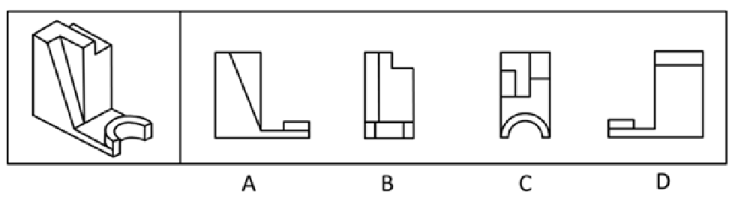
【解析】拓展3.课堂正确率为82%。问“不是”,A、D项轮廓一样,正面是A项,背面是D项,都可以看到,排除A、D项。
B项:如下角度可以看到,排除。
C项是从上往下观察,L型和矩形没有对齐,题干是对齐的,小横线位置不对,C项当选。【选C】