Appearance
属性规律
图形特征:元素组成不相同、不相似
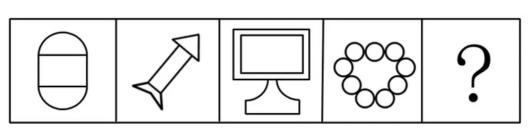
考点
1.对称性
2.曲直性
3.开闭性
如果参加国考,对称性几乎每年都会考到,曲直和开闭考查较少;如果参加省考,则三个考点的考频差不多。国考和省考都喜欢考对称性,但是国考不喜欢考曲直性、开闭性,省考比较喜欢考曲直性、开闭性。
考点一:对称性
TIP
1.轴对称:“等腰”元素出现

轴对称:中间画条线,两边长得一样。
2.中心对称:平行四边形、N、Z、S变形图出现、相同图形反着放

(1)如果出现平行四边形、“N、Z、S”及其变形图、相同图形反着放(如图二的图5),则考虑中心对称。
(2)五角星旋转180°后两个角朝上,原来是一个角朝上,正着看和倒着看不一样,所以五角星是轴对称图形,并不是中心对称图形。
3.轴对称+中心对称:存在相互垂直的对称轴
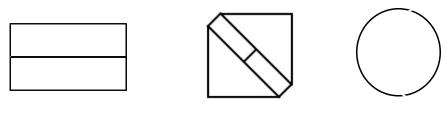
图1有横竖垂直的对称轴,图2有斜着垂直的对称轴,图3有无数条对称轴,存在横竖垂直的,都是轴+中心对称图形。
对称性的考法
1.区分对称类型:轴对称/中心对称/轴+中心对称
【例1】(2020四川下)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
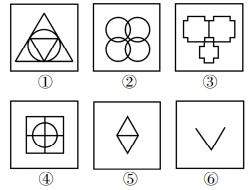
A.①②③,④⑤⑥
B.①③④,②⑤⑥
C.①②⑤,③④⑥
D.①③⑥,②④⑤
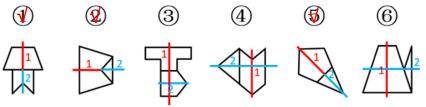
【解析】1.元素组成不相同,每幅图长得都不一样,优先考虑属性规律,图1出现等腰三角形,即“等腰”元素,优先考虑轴对称,当遇到轴对称时,一定要把对称轴画出来。图①有3条对称轴,是轴对称;图②有横竖垂直的对称轴,是轴+中心对称图形;图③有1条竖轴,为轴对称;图④有横竖垂直的2条对称轴,为轴+中心对称;图⑤有横竖垂直的2条对称轴,是轴+中心对称图形;图⑥只有1条对称轴,是轴对称图形。
因此,图①③⑥为一组,都是轴对称图形;图②④⑤为一组,都是轴+中心对称图形,对应D项。【选D】
2.对称轴的数量和方向
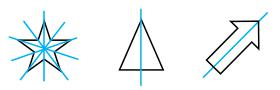
如果所有图形都是轴对称图形,则会考对称轴的数量和方向。如上图,图1五角星有5条对称轴,图2和图3都有1条对称轴,图1和图2对称轴的数量不同。如果数量相同,则可以考虑方向,图2和图3都有1条对称轴,图2到图3为顺时针旋转45°。所以,遇到轴对称图形,一定要把对称轴画出来。
【例2】(2024事业单位)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
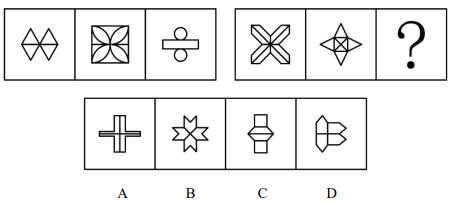
【解析】2.元素组成不相同,优先考虑属性规律,图1左右长得一样,为轴对称图形,第一件事是画出对称轴,第一组图都有横竖2条对称轴,图2斜着不对称,因为只有中间1条横线;第二组图都有横竖斜4条对称轴。
A项:有横竖2条对称轴,排除。
B项:有横竖斜4条对称轴,保留。
C项:有横竖2条对称轴,排除。
D项:有1条横轴,排除。【选B】
【注意】轴对称,一定要把对称轴画出来,接下来可以考虑对称轴的数量和方向。
3.对称轴与图形线、点、面的关系

【注意】如果对称轴的方向和数量没有规律,则考虑对称轴与原图线、点、面的关系:国考已经考过4-5次了,是必会的热门考点。
1.对称轴是否和线重合、是否经过交点、是否经过面、经过了几个面。
2.如上图,图1是横轴对称,内有1条横线和对称轴重合,图2没有线条和对称轴重合,看对称轴是否和线重合就是一种规律;图2对称轴会经过交点,图3对称轴没有经过交点,这也是一种规律;图2对称轴只经过了1个面,图3对称轴经过了2个面。
3.考试时依次按照线、点、面去看,是按考频高低进行排列的;考虑经过什么的时候线和点只需要看是否经过即可,可以不考虑数量,但是面一定会考查数量。
【例3】(2023江苏)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
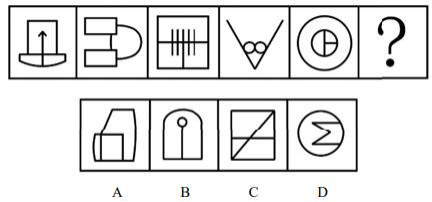
【解析】3.元素组成不同,优先考虑属性规律,图1左右长得一样,考虑轴对称,第一件事是画出对称轴,题干都是轴对称图形,A、C项排除,B、D项都是轴对称图形。
对称轴的数量都是1,方向也无规律,则考虑对称轴经过什么,先看线,线不行再看点,点不行再看面,图1、图3、图5对称轴均和某条线重合,图2、图4对称轴均没有和图形的线重合,则“?”处对称轴与图形的线应不重合,B项对称轴和图形的线重合,D项对称轴没有和图形的线重合,选择D项。
答疑:
(1)本题对称轴的方向依次为竖、横、竖、竖、横,无规律。
(2)不能按照“竖、横、竖;竖、横、竖”选择B项,这种看法是“天坑”,是把左边三幅图当成一组,右边三幅图当成一组,一组图只有两种看法,要么是从左往右观察,要么135一组、246一组,不能左边三幅图是一组,右边三幅图是一组,否则直接出成两组图的形式即可,所以一组图是不会从中间分开去观察的,这是错误的思维。【选D】
【注意】轴对称,先画出对称轴,考虑对称轴的数量和方向,如果对称轴的数量和方向没有答案,再考虑对称轴经过了什么。
【例4】(2023国考)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
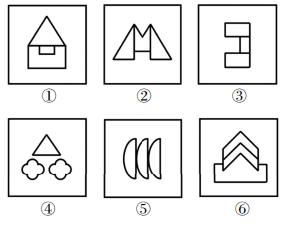
A.①③⑥,②④⑤
B.①③⑤,②④⑥
C.①②⑥,③④⑤
D.①⑤⑥,②③④
【解析】4.图1两边是等腰的,考虑轴对称,优先画出对称轴,对称轴的方向依次为竖、竖、横、竖、横、竖,对称轴的数量都是1,无法分组,有4条横轴、2条竖轴,也无法分组,根据对称轴的数量和方向均无法分为两组,考虑对称轴经过什么,对称轴没有经过某条线,图①②④⑤⑥的对称轴都经过交点,只有图③没有经过交点,据此也无法分组,考虑对称轴经过面。题干图形对称轴经过的面的个数依次为3、1、1、1、3、3。
因此,图①⑤⑥为一组,对称轴均经过3个面;图②③④为一组,对称轴均经过1个面,对应D项。
答疑:
(1)看线和点的时候不用关注数量,看面的时候一定要关注数量。图①对称轴经过1个点,图②对称轴经过1个点,图③原图中没有交点,经过0个点,图④对称轴经过1个点,图⑤对称轴经过2个点,图⑥对称轴经过3个点,没有规律,如果认为图①②④对称轴均经过1个交点,图③⑤⑥对称轴经过的都不是 1个交点,这不算规律,分组分类题只能有2组相同的数字,可以是“111、222”,不能是“111、023”。
(2)交点指的不是对称轴和图形产生的交点,而是原图本身就有的交点。图①原图最上边本身就有交点,画对称轴的时候会经过这个交点;图③原图本身就没有交点,对称轴也没有经过交点。【选D】
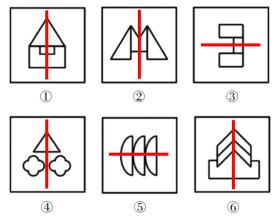
【注意】轴对称,一定要把对称轴画出来。
【注意】轴对称,一定要把对称轴画出来。
最“火”对称考法——对称轴经过的部分
1.线条重合/不重合(正中有线)
(2019国考)
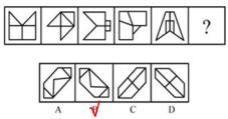
每幅图都是轴对称图形,画出对称轴,对称轴的方向有规律,每次顺时针旋转45°,“?”处对称轴的方向应为“左下-右上”,A、C项排除。剩余B、D项,对称轴与原图的线依次重合、不重合、重合、不重合、重合,选择B项,D项对称轴与原图的线有重合,排除。
(2020国考)
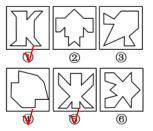
考查对称轴有没有经过交点,图①④⑤对称轴均没有经过交点,图②③⑥对称轴经过交点。
(2017河南)
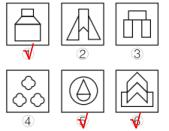
看对称轴和线重合无法分组,图①③④对称轴均没有经过交点,图②⑤⑥对称轴均经过交点,但是没有对应的选项。交点有规律,但是没有答案,考的是面,图①⑤⑥对称轴均经过1个面,图②③④对称轴均经过3个面。之所以要给大家拓展,是因为有的时候单独看一道题印象可能不深刻,本题和例 4的图形长得很像,国考是借鉴了2017河南真题,图形推理靠刷题,刷题刷得越多,正确率一定越高,每年都会有借鉴。
4.两个图形挨着或内外分开,分开看对称

两个图形挨着或内外分开,分开看对称。如上图,图1和图2都是 2个面挨着,整体不对称,考虑分开看,图1是2条横轴,2条对称轴平行,图 2是1条竖轴、1条横轴,2条对称轴垂直;图3和图4内外分开,可以分开看,图3里边是横轴,外边是竖轴;图4里边是横轴,外边是竖轴。
【例5】(2022联考)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
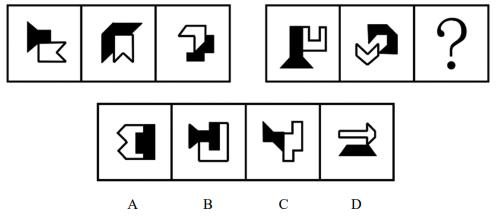
【解析】5.元素组成不同,优先考虑属性,每幅图中都有2个图挨着,考虑分开观察。第一组图,图1上下都是横轴,是平行的,图2上边是斜轴、下边是竖轴,相交45°,图3上下都是斜轴,是垂直的;第二组图2条对称轴的关系依次是平行、相交45°,则“?”处2条对称轴的关系应是垂直的。
A项:2条对称轴重合,排除。
B项:白色不对称,排除。
C项:2个图形都是中心对称,排除。
D项:有横竖2条对称轴,是垂直的,当选。【选D】
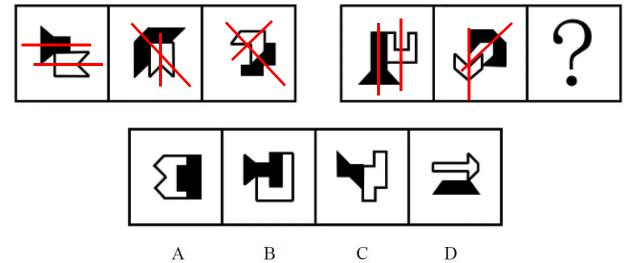
【注意】当2个面挨到一起或者分成内外2个部分,都要考虑分开看对称轴之间的关系。
(2022江苏)
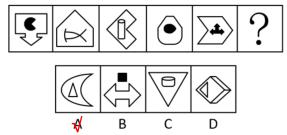
内外分开看,图1、图2里边是横轴、外边是竖轴,图3里边是竖轴、外边是横轴,图4里边是横轴、外边是竖轴,图5里边是竖轴、外边是横轴,内外对称轴都是垂直的,A项当选。
(2014上海)
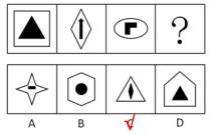
图1外部是正方形,有4条对称轴,内部有3条对称轴;图2外部有2条对称轴,内部有1条对称轴;图3外部有2条对称轴,内部有1条对称轴,考查外部对称轴的数量比内部1条,C项外部有3条对称轴,内部有2条对称轴,当选。既可以考对称轴之间的夹角,也可以考对称轴数量之间的关系。
(2018国考)
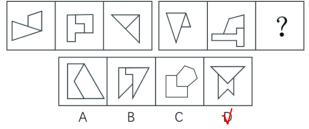
第一组图对称轴的关系依次为平行、相交45°、垂直,第二组图对称轴的关系依次为平行、相交45°,则“?”处2条对称轴应垂直,D项当选。
(2021浙江)
图①②⑤两条对称轴重合,图③④⑥两条对称轴垂直,据此分为两组。
(2022重庆选调)
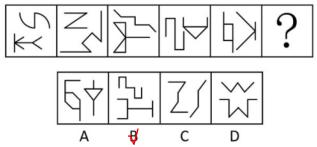
只要图形能够分成2个图形,都要有分开看思维。图1有2幅图,上边是“S”变形,是中心对称图形,下边是轴对称图形,题干中的2幅图有1个是轴对称、1个是中心对称。A项左边不对称,B项上边是中心对称图形,下边是轴对称图形,C项2个都是中心对称图形,D项2个都是轴对称图形,B项当选。
(2023国考)
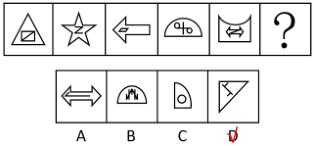
分成内外2个部分,内外分开看。外部都是轴对称,内部出现“Z”字,就是中心对称。A项内部不对称,B项内外都是轴对称,C项外部不对称,因为不是半圆,是椭圆的弧,线条不一样长,所以不对称,D项外部是轴对称,内部是中心对称,D项当选。
只要是两个图形,都可以分开考虑。
考点二:曲直性
特征图:出现明显的圆、弧等全曲线图,优先考虑曲直性
1.全直线

2.全曲线

3.曲+直
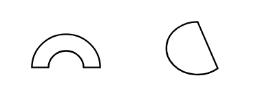
如果在曲直性部分做到分组分类题目,最严谨的考法是六个图中只出现这三种(全直线、全曲线和曲+直)里面的两种,如图①②③都是全直线图形,图④⑤⑥是全曲线图形;国考都是这么考,但是在省考中,可能会出题不严谨,例如会把全直线分在一组,把全曲线和有曲有直的放在一组,即一组是全直线,一组是有曲线,这种分法在国考上基本上不会考,但是省考出题不严谨,就会这么考查。
【例】(2023江苏)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。

【注意】
1.图形特征:元素组成不同——优先属性规律。
2.在考试中,如果发现题干图形大多为对称的,里面只有1~2个图形是不对称的,此时大概率考查曲直性。
【解析】
观察图形特征,元素组成不同,优先考虑属性规律,对称性考得多,优先考虑对称;第三行的图2是不对称图形,只要有一个图不对称,就不考虑对称性,考虑曲直性。第一列图形均为全曲线图形,第二列图形均为全直线图形,第三列图形均为有曲有直图形,则“?”处图形应有曲有直。
A项:为有曲有直图形,当选。
B项:为全直线图形,排除。
C项:为全曲线图形,排除。
D项:为全直线图形,排除。
【选A】
考点三:开闭性
特征图:出现生活化或粗线条图形,考虑开闭性
(1)生活化图形:例如,图一的图2、图二的图2均为“银行”的标志,图三的图2为“邮箱”的标志,即在生活中会遇到的图形,为生活化图形。
(2)粗线条图形:如图一,图1由细线条围成,但是图2的线条都很粗;如图二的图2,不是线条,而是一团团的黑色;这样的图形就是粗线条图形。
1.全封闭
2.全开放
3.半开半闭

在分组分类题目中,如果一组为全封闭图形,另一组为全开放图形是很严谨的考法;但是在省考中会出现不严谨的考法,如一组是全开放图形,把全封闭和半开半闭分到另一组,即一组是全开放图形,一组是有封闭图形。虽然我们参加的是国考,但是在未来自己刷题的时候会刷到一些省考不严谨的题目,所以在此提醒。
【例】(2024事业单位)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
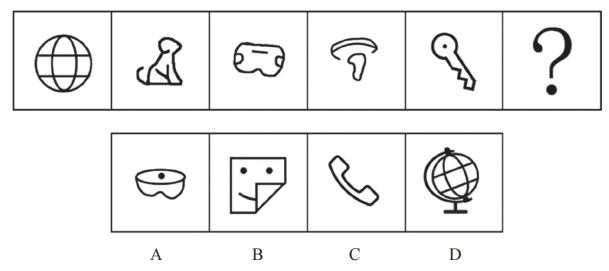
【注意】
1.图形特征:元素组成不同——优先属性。
2.右边是一团一团的黑色,为粗线条的图形。
【解析】
观察图形特征,元素组成不同,优先考虑属性规律,图2为不对称图形,所以不考虑对称性;考虑曲直性,图1为有曲有直图形,图2为有曲有直图形,图3为有曲有直图形,图4为全曲线图形,所以曲直性无规律;考虑开闭性,图1为全封闭图形,图2有封闭地方和外部出头端点,为半开半闭图形,图3为全封闭图形,图4有封闭地方和外部出头端点,为半开半闭图形,图5是全封闭图形,即图1、3、5为全封闭图形,图2、4、6有封闭,也有开放的地方,为半开半闭图形。
A、B、C项:均为全封闭图形,排除。
D项:有封闭地方和出头端点,为半开半闭图形,当选。
另一种思考方法:当出现生活化或粗线条图形,考虑开闭性。图2像“小狗”趴着;图5像“钥匙”;C项像“电话”,D项为“地球仪”,这些均为生活化图形,可以优先考虑开闭性。
答疑:本题不能考虑曲直性,因为图1、2、3均为有曲有直图形,但是图4只有曲线,没有直线,所以曲直性没有规律。【选D】
属性规律总结
一、属性类识别特征:元素组成不相同、不相似
二、对称性:
1.“等腰”元素:优先轴对称
2.平行四边形、S、N、Z变形图、相同图形反着放:优先中心对称
3.有相互垂直的两条对称轴:轴+中心对称
识别题型→画出对称轴→考虑数量、方向→对称轴与线、点、面的关系)
三、曲直性:全曲、全直、曲+直
四、开闭性:全开、全闭、半开半闭