Appearance
数量规律
“数量规律”图形特征
(1)元素组成不同,且属性没规律
(2)数量特征图明显
考点
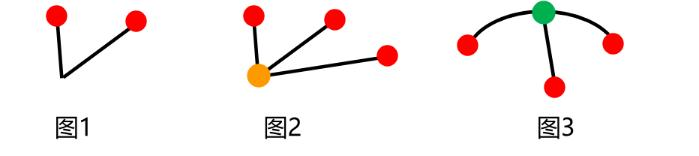
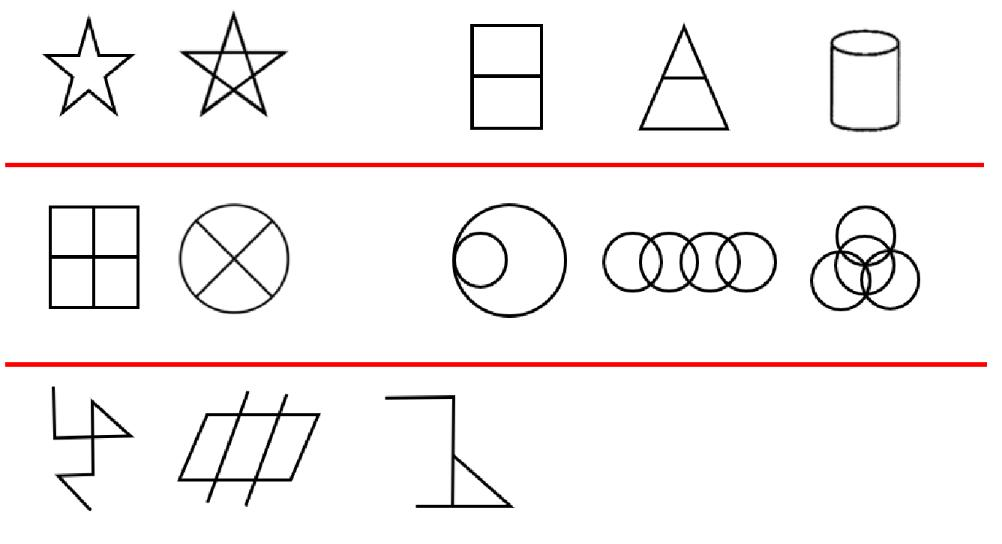
点、线、角、面、素
考点一:面数量
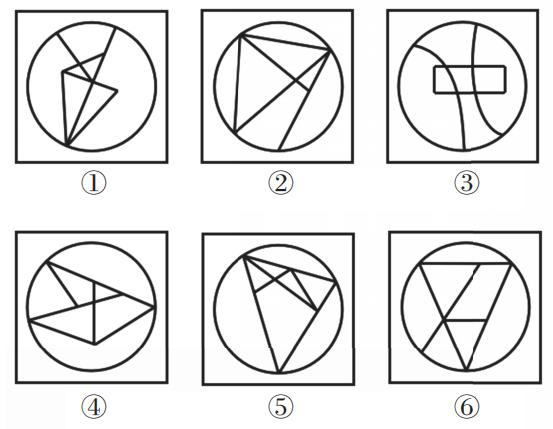
1.什么是面?白色的封闭区域
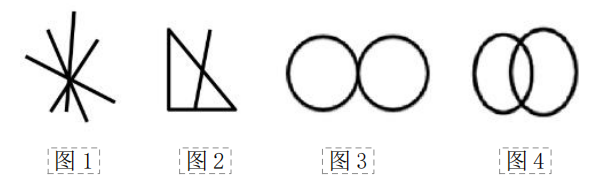
图1外面有白色的封闭区域,有1个面;图2的线条没有封闭起来,有0个面;面是白色的封闭区域,只有中间的三角形封闭区域是一个面,黑色的部分不是面,所以图3有1个面。
面是白的,黑的不是面!
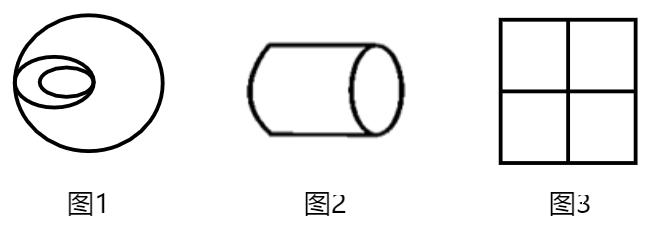
2.什么时候数面?
(1)图形被分割、封闭面明显
①图形被分割。图1的外面有一个边框,里面用线将其分割成不同面,此时可以优先考虑数面。
②封闭面明显:图2里面都是窟窿,都是面,此时叫作封闭面明显,可以数面。
(2)生活化图形、粗线条图形

如图1像“齿轮”,图2像“火车头”或“直升飞机”,为生活化图形,且图形里面出现一团团黑色,为粗线条图形;遇到这种生活化、粗线条图形可以优先数面。图1的白色部分是面,所以有1个面;图2有5个面。
生活化图形可以考查开闭性和面数量。
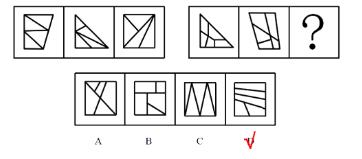
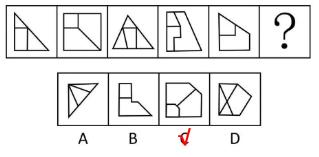
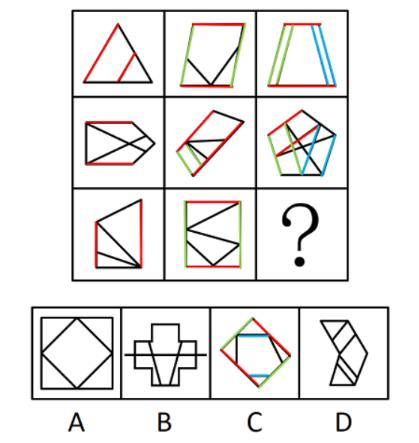
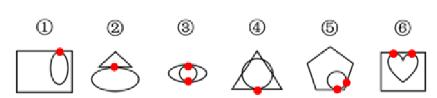
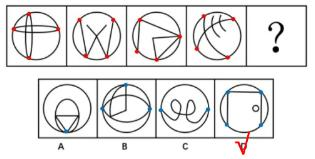
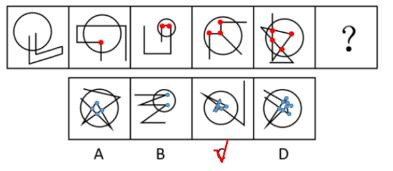
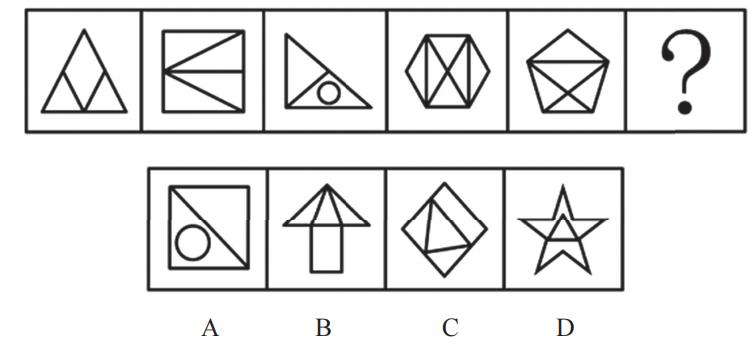
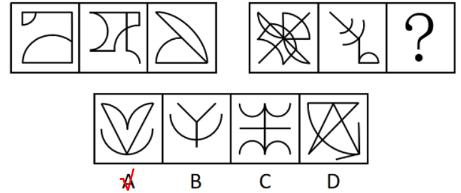
【例1】(2023重庆选调)
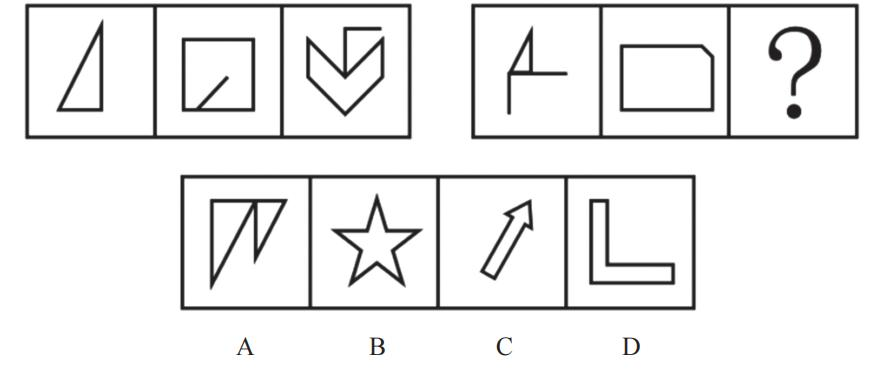
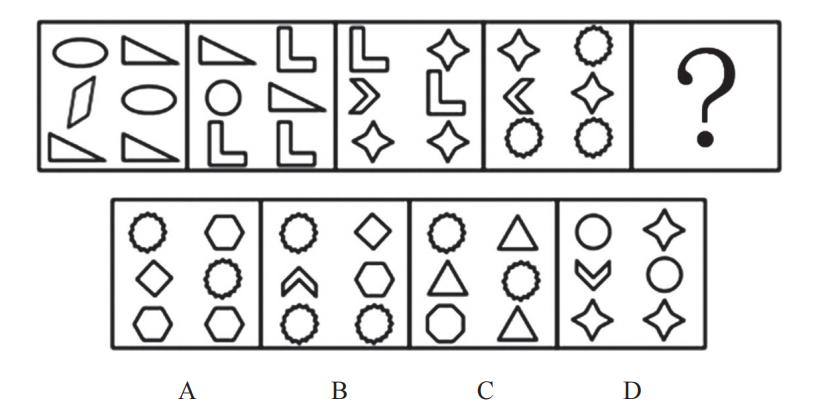
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
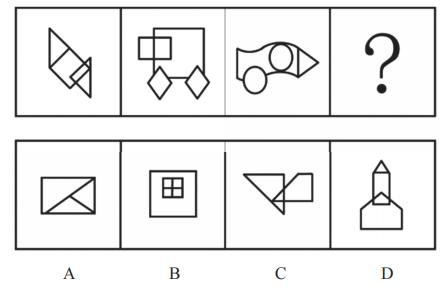
【解析】1.观察图形特征,每个图不一样,元素组成不相同,优先考虑属性规律。图1不对称,不能考虑对称性;图1、2为全直线图形,图3为有曲有直图形,所以曲直性无规律;题干和选项均为全封闭图形,所以开闭性虽然有规律但是无答案,属性没有规律,考虑数量规律。出现窟窿和面,考虑面数量。
题干图形面数量均为5个,则“?”处图形的面数量为5个。
A项:有3个面,排除。
B项:有5个面,当选。
C项:有4个面,排除。
D项:有4个面,排除。【选B】
【注意】
1.图形特征:元素组成不同——优先属性。
2.图形特征:封闭面明显——优先数面。
3.思考规律的先后:当拿到一道题目发现图形的封闭面均特别明显、都是窟窿、都是面,此时可以不优先考虑属性规律,可以优先数面;当遇到难题没有思路的时候,可以优先考虑属性规律再考虑数量规律。
面的细化考法
【注意】面的细化考法:直接数面的题目比较简单,考查较少,目前考试较流行的考法是以下三种。如果整体数面无答案,考虑面的细化,共有三个角度。
1.所有面的形状(三角形、四边形)
观察图形里面是否有三角形/四边形面,如果有,观察有几个。如图,图1有3个面,均为三角形的面;图2有3个面,其中有2个三角形的面;图3中没有三角形的面(0个)。
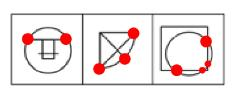
2.相同面的数量(“双胞胎”“多胞胎”)
相同面指的是面的形状和大小一模一样,即“双胞胎”“多胞胎”面。如图,如图1中有2个长得一模一样的面(直角三角形),图2有2个长得一模一样的面(三角形);图3中有5个面长得一模一样。
3.最大/最小面的形状、属性(对称、曲直)、与外框的关系(相似、边相等)
找最大面/最小面的时候,最先找最大面,因为最大面比较直观且考查多;如果最大面有规律继续看,如果最大面无规律再看最小面。
(1)形状:最大面是几边形。如图,图1中最大面是三角形,图2最大面是四边形(有4条边)。
(2)属性:主要看对称和曲直,因为面是封闭的,不用看开闭性。
①对称性。如图,图1最大面是等腰三角形,最大面为轴对称图形;图2最大面是平行四边形,最大面为中心对称图形,图3最大面是圆(有横轴、竖轴和垂直的对称轴),最大面为轴对称+中心对称图形。
②曲直性。如图,图1和图2最大面是由直线组成的,图3最大面是由曲线围成的。
(3)与外框关系:主要看最大/最小面与外框是否相似、与外框边的数量是否相等。如图,图1最大面是三角形,外框是四边形,那么最大面和外框不相似,外框边数也不相等;图2最大面是平行四边形,外框是正方形,最大面与外框不相似,但是与外框边数量相等;图3最大面和外框均为圆,即最大面和外框相似。
在国考和省考中简单题不多,大多数题目都比较难,如2025年国考考查最大面都是轴对称图形,所以以上的知识必须会。如果觉得学习的知识太多、记不住,就把这些知识抄下来,每天背一下,在考试的时候这些考点不是临时想到的,都是背下来的。如果把上述知识都背下来,也不一定全部题目都能做出来,在考试中90%的题目会做出来,另外10题中有1题大约为创新题。目前是打基础的阶段,只要把基础考法学会了,就学会了90%,就够用了。
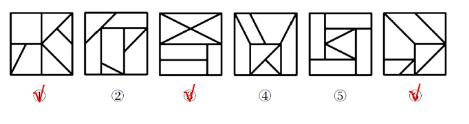
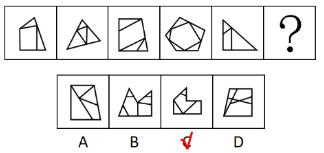
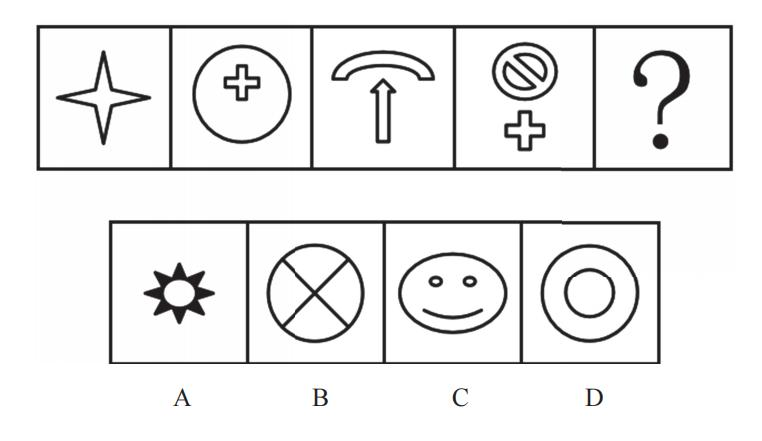
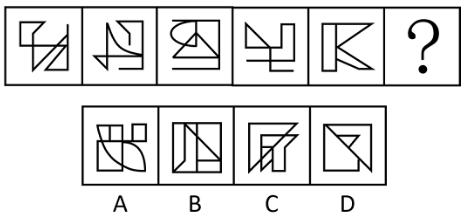
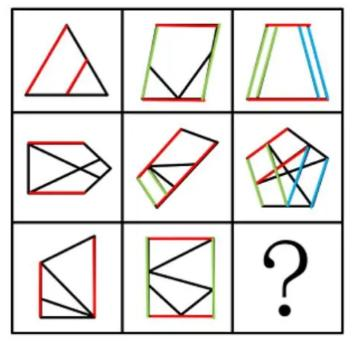
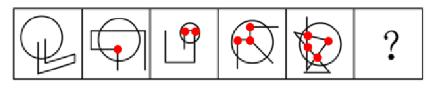
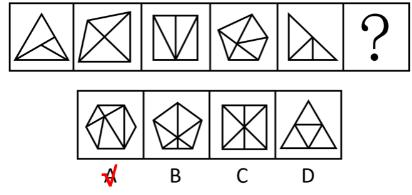
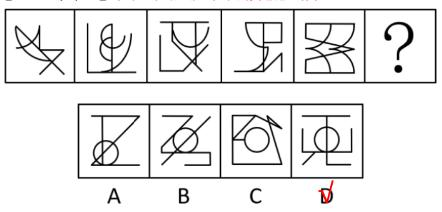
【例2】(2021浙江)
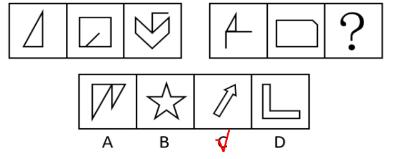
从所给的四个选项中,去掉哪一个后,剩下的图形序列可以呈现一定的规律性?
【解析】2.问“从所给的四个选项中,去掉哪一个后,剩下的图形序列可以呈现一定的规律性”,注意问法。做题思维一样,图1的外框是一个正方形,里面用线分割成不同的面,即图形被分割,封闭面明显,优先数面。题干和选项的面数量都是3个,没有办法做题,考虑面的细化,第一个先看所有面(里面是否有三角形面)、第二个看是否有长得一样的面,第三个看最大/最小面。
图1有2个三角形面;图2有2个三角形面;A项中有2个三角形面;B项中有3个三角形面;C项中有2个三角形面;D项中有2个三角形面,根据三角形的面数量去掉B项(3个),其余的图形中三角形的数量均为2个,B项当选。
这种题目近几年考查得很多,国考也会考查。【选B】
【注意】
1.图形被分割、封闭面明显——优先数面。
2.面的细化——所有、相同、最大/最小。
所有面—重点关注三角形、四边形
(2019北京)
题干图形外边框被分成不同的面,可以考虑数面。第一组图均为4个面,第二组图均为5个,但是四个选项的图形均为5个面。虽然数面有规律,但是选不到答案,此时可以观察三角形/四边形的数量,第一组图中的4个面都是三角形的面,第二组图的5个面全部都是四边形的面;A、B、C项中的图形均有三角形,均排除;D项中5个面都是四边形,选择D项。
(2022国考)
题干图形外部为正方形,里面用线将其分割成面,封闭面特征明显,优先数面。题干图形均为7个面,没有办法分组,考虑三角形的面,图①③⑥为一组,均有4个三角形的面;图②④⑤为一组,均有3个三角形的面。
一般关注三角形的面就可以,四边形的面考查少,如果一道题三角形的面没有规律,此时可以考虑四边形的面,另外如果一道题中没有三角形的面,一般也不会考查四边形的面,所以在做题的时候重点观察是否有三角形的面。
按照以下顺序进行验证,先看三角形的面,再看相同面,再看最大/最小面。
【例3】(2024事业单位)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】3.观察图形特征,出现窟窿和面,考虑数面。题干图形面数量依次为5、4、4、3、3、?,面数量无规律,从三个角度思考。
第一个看所有面里是否有三角形的面,图1、2、3有三角形的面,但是图4、5没有三角形的面,所以三角形的面无规律。第二个看图形里面是否有长得一模一样的面,图1有2个直角三角形长得一模一样,图2有2个圆长得一模一样,图3有两个三角形长得一模一样,图4中有两个圆长得一模一样,图5中上面2个六边形的形状和大小长得一样,但是下面的图虽然也是六边形,但是和上面的图不一样,有些“瘪”,所以图5有2个面长得一模一样,则“?”处图形应该有2个相同面。
A项:没有相同面,排除。
B项:左边和右边的面长得一样,有2个相同面,保留。
C项:没有相同面,排除。 D项:没有相同面,排除。【选B】
【注意】
1.封闭面明显——优先数面。
2.面的细化——所有、相同、最大/最小。
相同面——关注形状大小都一样的面
(2020新疆)
本道题很看细节,图形里面都是面,优先考虑数面。图①有4个面,其余图形面数量均大于4,所以数面没有规律;图①没有三角形的面,所以三角形的面没有规律;看相同面,图①中有4个相同面,图②有6个相同面,图③有6个面长得一样(最下面的面是六边形,其余的图形为五边形),图④有6个面长得一样,图⑤中有4个圆长得一样,图⑥中有4个长方形长得一样,即图①⑤⑥为一组,有4个相同面;图②③④为一组,有6个相同面。
(2022北京)
题干图形外面为一个边框,里面由线分割成不同个面,优先考虑数面。题干图形面数量均为4个,无答案,考虑面的细化。题干图形中没有三角形的面,考虑相同面,图1中有2个长方形长得一样,图2中有2个三角形长得一样,图3中有2个“鞋子”形状的图形长得一样,图4中有2个“L”形状的图形长得一样,图5中有2个相同面,即题干图形均有2个相同面,则“?”处图形应该有2个相同面,B项当选。
相同面指的是形状、大小、面积都一模一样。如例3中的C项中的2个三角形长得不一样,一定要是大小和面积都一样的才是相同面。
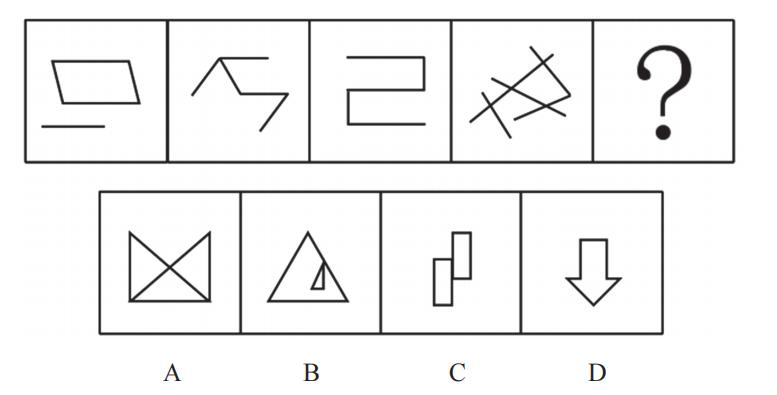
【例4】(2024联考)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
A.①③④,②⑤⑥
B.①③⑤,②④⑥
C.①⑤⑥,②③④
D.①④⑥,②③⑤
【解析】
4.观察图形特征,题干图形外框为正方面,内部用线将正方形分成不同面,所以优先考虑数面。图①②③④均为5个面,当数到第4个面的时候就不用再数了,因为无法分成两组,整体数面无规律,可以考虑面的细化(三角形的面、相同面和最大/最小面)。
图①中没有三角形面、没有相同面、有最大面(“Z”字形),当遇到平行四边形、“S、N、Z”变形、相同图形反着放要考虑中心对称,所以图①的最大面为中心对称图形;图②最大面为轴对称图形;图③最大面为轴对称图形,图④最大面为轴对称图形;图⑤最大面(“Z”字形)为中心对称图形;图⑥最大面为平行四边形,为中心对称图形。
故图①⑤⑥为一组,最大面为中心对称图形;图②③④为一组,最大面为轴对称图形,C项当选。【选C】
【注意】
1.图形被分割、封闭面明显——优先数面。
2.面的细化——所有、相同、最大/最小(几边形、属性、与外框关系)。
3.一个图形是否有三角形面、相同面、最大/最小面都很快能做好,只要把老师告诉的特征记熟练了做题就会快了,最怕做题的时候记不住老师所讲的图形特征和考点。
【2024浙江】最大面边数
考查最大面边数。题干图形都有面,但是数面无规律,图5中没有三角形面,题干图形也没有一样的面,考虑最大/最小面,最大面依次为三边形、四边形、五边形、六边形、七边形,则“?”处图形最大面应为八变形,选择B项。
【2024联考】最大面轴对称/中心对称
题干图形均有5个面,选不出唯一答案,图1没有三角形面、相同面,但是有最大面,最大面为中心对称图形,故图①⑤⑥为一组,最大面为中心对称图形,图②③④为一组,最大面为轴对称图形。
【2023联考】最小面与外框相似
最小面与外框相似。题干图形均有面,但是整体数面没有规律,图2中没有三角形面,图1没有相同面,所以关注最大面/最小面。图1有最大面,但是图2有两个一模一样的面,没有最大面,最大面指的是最大的、唯一的面,此时看最小面。题干图形最小面的形状依次为三角形、四边形、三角形、四边形、四边形,最小面形状无规律,另外图4和图5最小面为直角梯形,不对称,所以对称性无规律,此时考虑最小面与外框形状关系,题干图形的最小面均与外框相似,C项当选。
【2022联考】最大面边数与外框相等
题干图形数面特征明显,优先考虑数面,数面无规律;题干图形虽然有三角形的面,但是三角形的面数量依次为2、4、3……,三角形面数量无规律,另外图1中无相同面,看最大/最小面。最大面的形状依次为四边形、三角形、四边形、五边形、三角形,故最大面的形状无规律,考虑最大面的对称性,图1的最大面不是对称的,对称性无规律,考虑最大面与外框关系。图1最大面和外框均为四边形,图2最大面和外框均为三角形,图3最大面和外框均为四边形,图4最大面和外框均为五边形,图5最大面和外框均为三角形,即题干图形最大面和外框边数相同,C项当选。
这些考点较难,只要把这四个考点背下来,考试的时候就能想到,图形最难的就是没有见过,课下要多抄多背,有的同学笔记记得很详细,考高分的概率就大。
数面特征明显、整体数面无规律——考虑细化考法
1.所有面的形状
2.相同面的数量
3.最大/最小面的形状、属性(对称、曲直)、与外框的关系(相似、边相等)
考点二:线数量
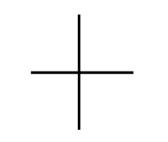
1.什么是线?
直线
曲线
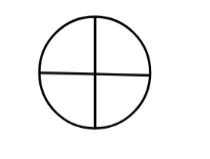
2.什么时候数线?
直线特征图:多边形、单一直线
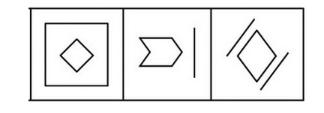
图1的正方形是独立的多边形;图2和图3均有单一直线。
曲线特征图:曲线图形(圆、弧、单一曲线)
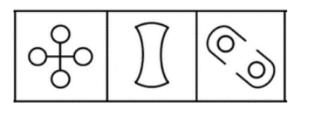
图3左右均是独立存在的圆,均是单一曲线。
【例1】(2022湖北选调)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】
1.题干出现多边形,考虑数直线;题干的图2和图4均有独立存在的圆,有单一曲线,考虑数曲线,哪个有规律用哪个。直线数依次为8、12、7,无规律;曲线数依次为0、1、2、3,故“?”处有4条曲线。
A项:没有曲线,排除。
B项:一个圆就是平滑的1条曲线,排除。
C项:有4条曲线,当选。
D项:两个圆有2条曲线,排除。
答疑:线指的是细的线条,A项中间没有细的线条,没有线。【选C】
【注意】
1.图形特征:单一曲线——优先数曲线。
2.一道题目既有数直线和数曲线的特征,优先考虑数曲线(考查较多),数直线的题目考查较少。
【例2】(2023事业单位)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】2.题干的图1出现单一直线、多边形,考虑数直线,题干图形的直线数均为5,故“?”处有5条直线。
A项:有5条直线,保留。
B项:有6条直线,排除。
C、D项:有7条直线,均排除。【选A】
【注意】
1.图形特征:单一直线、多边形——优先数直线。
2.听课听得懂,但做题不会是因为解题思路没有跟上,最难的是需要背下来图形特征,这样就知道考虑什么考点。
(2024四川)
每幅图均分内外,内外均出现独立的多边形,考虑数直线,内外边数量依次为6、4、3、7、5,内外边数量相等,四个选项的外部边数量均是六边形,找内部是六边形的选项,D项内部是六边形,内外都是6条边,当选。
(2022联考)
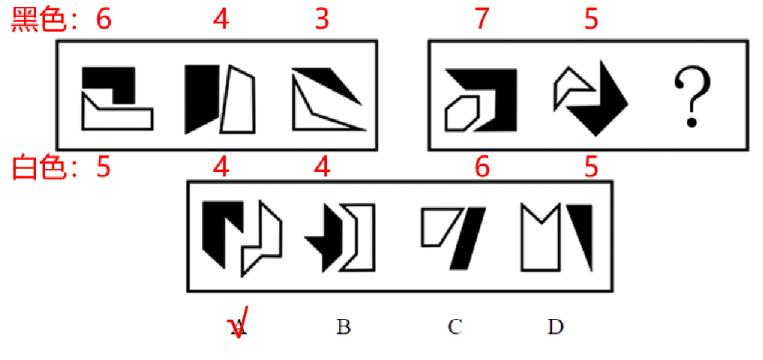
每幅图均由2个图形组成,考虑内外分开看;每幅图均有多边形,考虑多边形有几条边。第一组图,黑色边数依次为6、4、3,白色边数依次为5、4、4,相加无规律,考虑相减,黑色-白色边数依次为1、0、-1,规律为等差数列;第二组图,黑色-白色边数依次为1、0,故“?”处黑色-白色边数为-1,即黑色比白色少1条边,A项当选。
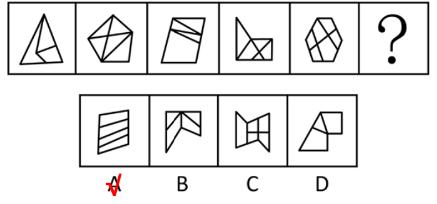
【例3】(2019浙江)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
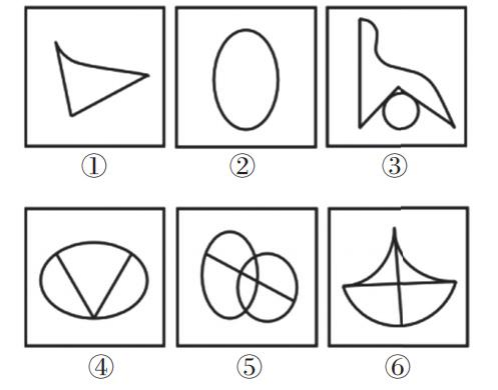
A.①③④,②⑤⑥
B.①③⑥,②④⑤
C.①②③,④⑤⑥
D.①④⑤,②③⑥
【解析】
3.除了图②(只有直线)外,其余图形均有曲有直,考虑数曲线、直线,单独数可以做出来,则直接做;单独数做不出来,则考虑做运算。图形有直有曲,优先数曲线(考查较多),曲线数依次为1、1、2、1、2、3,无规律;考虑数直线,直线数依次为2、0、3、2、1、2,无规律,考虑做运算。
因此,图①③④为一组,曲线比直线均少1;图②⑤⑥为一组,曲线比直线均多1,A项当选。
答疑:
(1)数面很少有曲线图,大多数都是直线。
(2)图③没有外框,无法区分内外。【选A】
【注意】图形特征:大多数图都有曲有直——数曲线、直线,可能做运算。
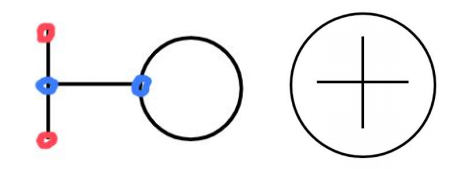
线的特殊考点:笔画数
1.什么是一笔画?在不能重复的情况下,能够一笔画成
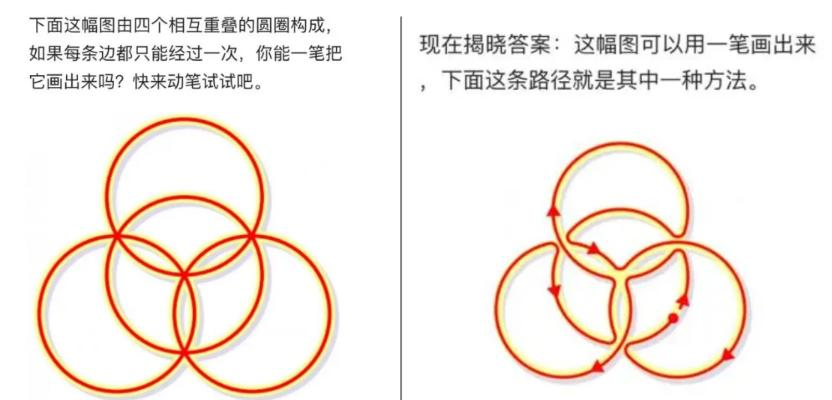
2.怎么判断一笔画?
(1)线条之间连通
(2)奇点数量为0或2
(奇点:以一个点为中心,发射出奇数条线)
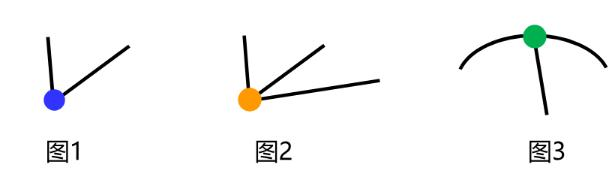
端点也是奇点,不要忘记数!
多笔画
笔画数=奇点数/2(奇点数一定是偶数个)
(1)如图一,红点都是端点,都是奇点;2个蓝点分别发射3条线,分别是奇点,共有4个奇点,超过2个奇点,4÷2=2,为两笔画图形。
(2)奇点数只能是偶数个,不可能是奇数个。如果数出5个奇点,5÷2=2.5,不可能有这种情况。
2.图形不连通,需要看成两个图,分开计算笔画数。如图二,内部有4个奇点,为两笔画;外部是一个圆,为一笔画,相加共三笔画。
笔画数常见特征图
(五角星、“日”、“田”、圆相切/相交及变形图、多端点)
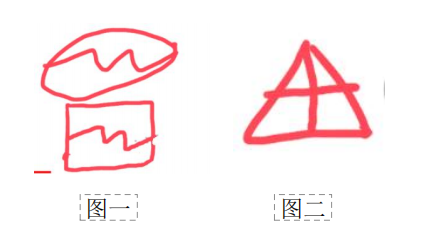
【注意】笔画数常见特征图: 1.五角星。
2.“日”“田”字及其变形图:
(1)“日”字变形:外框可以变形为长方形、正方形、三角形、有直有曲的、弧线,本质是内部1条线+1个外框。如图一,均是“日”字变形,一笔画图形。
(2)“田”字变形:1个外框(可以是曲线、三角形)+内部1个“十”字。如图二,为“田”字变形。
3.圆相切/相交及其变形图:圆相切或套圈。只要是封闭图形套圈(如2个正方形)或用点连着即可。
4.多端点:出头端点。笔画数中至少有50%的题目都会出现多端点。
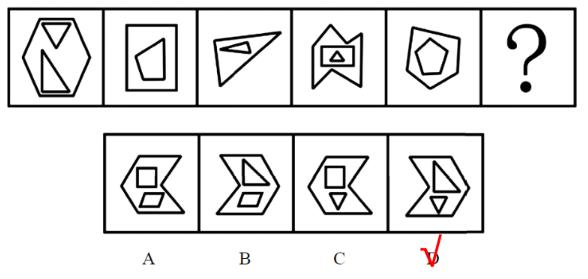
【例5】(2025国考)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
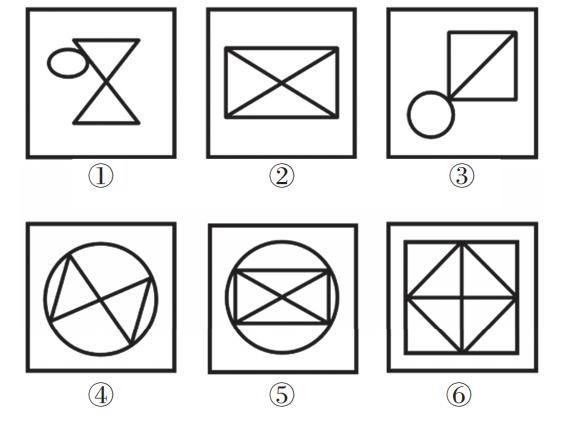
A.①②④,③⑤⑥
B.①③④,②⑤⑥
C.①②⑤,③④⑥
D.①④⑤,②③⑥
【解析】5.图①出现相切,图②内部“十”字,外部是边框,“田”字变形,图③右上角是“日”字变形,优先考虑笔画数,数奇点。图①有0个奇点;图②有4个奇点;图③有2个奇点(左下角的点发射出5条线);图④有0个奇点;图⑤有4个奇点(均发射出5条线);图⑥有4个奇点(均发射出5条线)。
因此,图①③④为一组,均是一笔画图形;图②⑤⑥为一组,均是两笔画图形,B项当选。【选B】
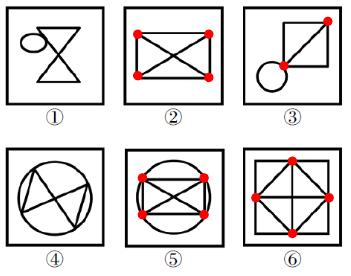
【注意】
1.图形特征:圆相切、“日”“田”变形——优先笔画数。
2.去框法数笔画:
(1)如图一,内部1条线,是一笔画,加上1个外边框,仍为一笔画。
(2)如图二,去掉外边框,内部的“×”是两笔画,整体为两笔画。
(3)如图三,去掉外框,内部类似倒着的“8”,为一笔画,整体为一笔画。
(4)如图四,去掉外框,内部的“×”是两笔画,整体为两笔画。
【例6】(2023国考)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
A.①③⑤,②④⑥
B.①④⑥,②③⑤
C.①③④,②⑤⑥
D.①②④,③⑤⑥
【解析】6.图③⑥均有出头端点,图①②均为“日”字变形(外框+内部1条线),考虑笔画数。图①②均有2个奇点,一笔画;图③⑤有4个奇点,两笔画;图④有2个奇点,一笔画;图⑥有2个奇点,内外分别是一笔画,共两笔画。
因此,图①②④为一组,均是一笔画图形;图③⑤⑥为一组,均是两笔画图形,D项当选。【选D】
【注意】
1.图形共考查10道题,笔画数可能在倒数1/2/3道题中考查。
2.图形特征:“日”字变形、多端点——优先笔画数。
【2023国考1】
【2023联考】
【2023北京】
【2023国考2】
【2022国考】

【2022联考】
【注意】
1.一道题有2-3幅图有端点,考虑笔画数。
2.“日”字和“田”字变形,考虑笔画数。如2022年国考,图①是“日”字变形,图⑥是“田”字变形。
3.面与面之间用点连接,考虑笔画数。如2022年联考,图①用1个点连接2个三角形;如2022年国考,图④用1个点连接三角形;如2023年国考2,图⑥右下角用1个点将三角形与别的图形连接。
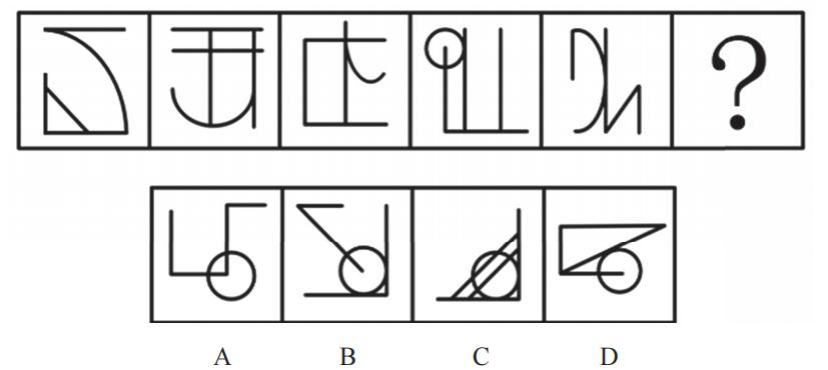
【例4】(2022江苏)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。

【解析】4.图形特征是笔画数,第一行,图1是“日”字变形;第二行,图1是“田”字变形,图3是五角星+外框;第三行,图1和图2均是“日”字变形(外框+内部1笔画成),考虑笔画数,第一行,笔画数依次为1、1、2;第二行,笔画数依次为2、2、1,笔画数无规律,考虑平行线。第一行,平行线组数依次为1、2、3;第二行,平行线组数依次为1、2、3;第三行,平行线组数依次为1、2,故“?”处有3组平行线。
A项:有4组平行线,排除。
B项:有2组平行线,排除。
C项:有3组平行线,保留。
D项:不止有3组平行线,排除。【选C】
【注意】
1.图形特征:“日”字、“田”字变形——优先笔画数。
2.笔画数没规律——可以考虑平行线。
【2022江苏】
【2021浙江】

第一组图,图1是“日”字变形,图2有多端点,图3的三角形与其他图形用点连接,考虑笔画数,笔画数依次为1、3、1,无规律,考虑平行线。第一组图,均有2组平行线;第二组图,均有3组平行线。
【2024江苏】
每幅图均有出头端点,考虑笔画数,笔画数依次为1、1、2、2,无规律,考虑平行线。
有笔画数特征,但无规律——先看平行线、再数交点
线数量小结
1.线数量考点: 直线、曲线、笔画问题
2.什么时候数线
(1)直线数特征图:多边形、单一直线
(2)曲线数特征图:曲线图形(单一曲线、圆、弧)
3.笔画问题
(1)笔画数特征图:多端点、圆相切/相交、日、田、五角星
(2)一笔画条件:连通图+奇点数为0或2
(3)多笔画公式:奇点数÷2
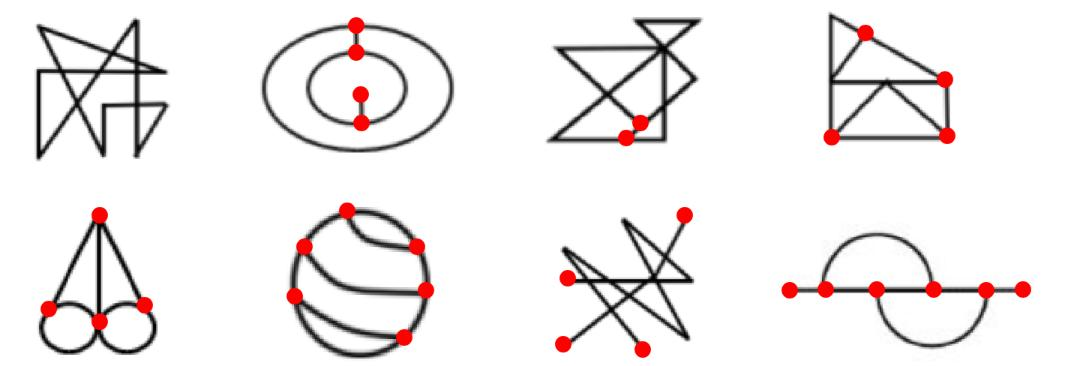
考点三:点数量
1.什么是点?线与线的交点
注:切点也属于交点
2.什么时候数点?
点数量特征图:
(1)线条交叉明显(俗称“大树杈)
(2)多边形或圆中叉出一些线条
(3)圆相切或圆相交较多
点数量的特征图和笔画数的特征图很像,比如图1、图2能够想到端点,图3、图4能够想到多圆相交/相切,点数量的题目都比较难,正确率在50%左右,如果存在笔画数的特征(五角星、“日”“田”变形、多圆相交/相切、多端点),考虑笔画数,但是笔画数无规律,先看平行线、再数交点。
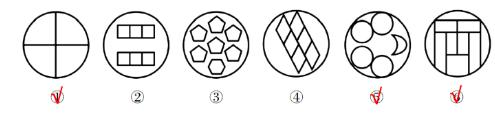
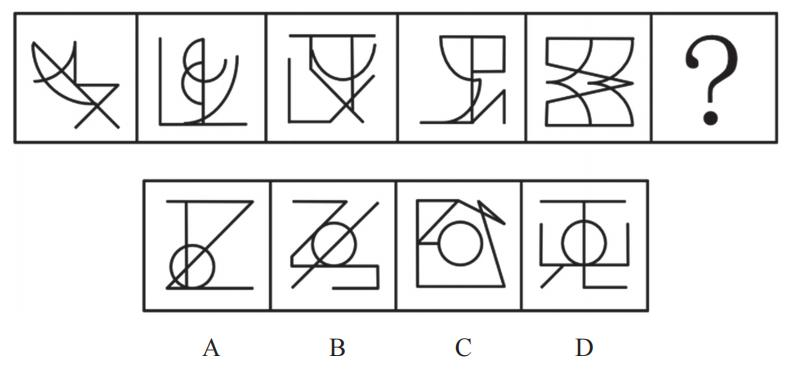
【例1】(2020山东)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】1.第一组图2、图3以及第二组图1都有出头端点,A项是三角形用点与其他图形连着,B项是五角星,可能考查笔画数,第一组图都是一笔画,第二组图的笔画数依次为2、1,笔画数无规律(不可能下一幅图是0笔画);第一组图1没有平行线,平行线也无规律,考虑交点数。
第一组图的交点数依次为3、5、7,等差数列;第二组图的交点数依次为3、5,则“?”处图形应有7个交点。
A项:有5个交点,排除。
B项:有10个交点,排除。
C项:有7个交点,当选。
D项:有6个交点,排除。【选C】
【注意】多端点——笔画数、平行线、交点。
(2020山东)
(2020青海)
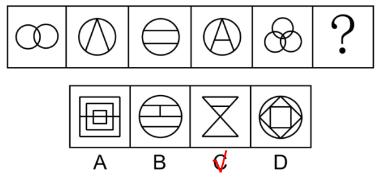
图1、图5是圆相交,考虑笔画数,题干图形的笔画数依次为1、1、2、2、1,笔画数没有规律;考虑平行线,图1没有直线,则没有平行线;考虑交点,题干图形的交点数量依次为1、2、3、4、5、6,则“?”处图形应有7个交点,选择C项。
点的细化考法
①切点:
图一
②框上/框内交点:
图二
③曲直交点:
图三
大部分图都有圆或椭圆或圆弧椭圆弧,可优先考虑点的细化
切点一般要有直线和曲线相切,至少要有曲线;曲直交点也要有曲线;目前省考、国考考查框上/框内交点一般都是考查圆,正方形考得非常少,因此大部分图都有圆或椭圆或圆弧、椭圆弧时,优先考虑点的细化。做题时优先考虑切点,因为有没有切点一眼就能看出来;如果切点没有规律,则关注有没有框,要考查框上/框内交点,一定会有框,都有框时考虑框上/框内交点(如图二,都有圆框,圆内交点数依次为0、1、2、3、4,“?”处应有5个框内交点),只要有1幅图没有框就考虑曲直交点(如图三,图1、图3有圆框,但图2没有圆作为框)。
【例2】(2024联考)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】2.每幅图都有曲有直,但不是每幅图都有圆作为框,无法考查框上/框内交点,考虑切点、曲直交点。图1将上方的横线延长,将半圆画出来,发现左上角是弧和直线的切点;图2将半圆补充完整,发现右侧是切点;图3补充成完整的椭圆,发现存在切点;题干每幅图都有1个切点。
A项:没有切点,排除。
B项:有2个切点,排除。
C项:有2个切点,排除。
D项:有1个切点,当选。【选D】
【注意】每个图都有曲有直——交点(切点、曲直交点)。
【例3】(2022天津)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
A.①②③,④⑤⑥
B.①④⑤,②③⑥
C.①②⑥,③④⑤
D.①③⑥,②④⑤
【解析】3.每幅图都有圆,优先考虑切点,其次考虑框上/框内交点,最后考虑曲直交点。图①没有切点,则考虑圆上/圆内交点,图①圆上有3个交点,图②圆上有4个交点,图③圆上有4个交点,图④圆上有3个交点,图⑤圆上有3个交点,图⑥圆上有4个交点。
因此,图①④⑤为一组,都有3个圆上交点;图②③⑥为一组,都有4个圆上交点,选择B项。【选B】
【注意】每个图都有圆——交点(切点、框上/框内交点、曲直交点)。
【2018广州】框上交点
【2022天津】框上交点
【2019浙江】框内交点
【2018国家】框内交点
【注意】2018广州、2022天津都是考查圆上交点,2019浙江、2018国家都是考查圆内交点,对比区别,发现考查框上交点时圆的外边没有线,而考查框内交点时圆的外边有很多出头线条,这是刷题之后总结出来的经验,出头时优先考虑内部,没有规律时再考虑框上;没有出头时优先考虑框上,没有规律时再考虑框内。
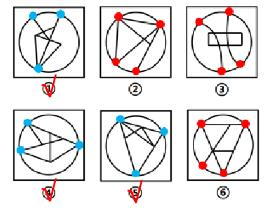
【例4】(2023湖北)
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
A.①②③,④⑤⑥
B.①②⑤,③④⑥
C.①③④,②⑤⑥
D.①④⑤,②③⑥
【解析】4.每幅图都有曲有直,但图①没有圆、椭圆作为框,无法考查框上/框内交点,考虑切点、曲直交点;图①没有切点,则考虑曲直交点。
图①有6个曲直交点;图②有9个曲直交点;图③有6个曲直交点;图④有6个曲直交点;图⑤有9个曲直交点;图⑥有9个曲直交点。
因此,图①③④一组,均有6个曲直交点;图②⑤⑥一组,均有9个曲直交点,选择C项。【选C】
【注意】每个图都有曲有直——交点(切点、曲直交点)。
点数量小结
1.什么是点:
线与线的交点
2.点数量特征图:
线条交叉明显(一般有笔画特征)
3.点数量细化考法:
切点、框上/框内交点、曲直交点
考点四:素数量
1.什么是素?独立小图形
图一
2.出现小元素,做题思路?
(1)优先考虑元素种类和个数
(2)找相同元素
颜色不同,一般为两种
大小不同,一般为一种
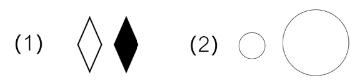
图二
【注意】素数量:
1.什么是素:独立小图形。
2.出现小元素,做题思路:
(1)优先考虑元素种类和个数:个数就是有几个图形;长得一样的算1种,如图一,图1的2个星星是1种,图2的2个圆形是1种,总共有2种,图3的2个菱形是1种,总共有3种,元素种类和个数比较简单,考得很少。
(2)元素种类和个数选不出唯一答案,考虑找相同。
①内部找相同:比如图一中图1有2个长得一样的元素、图2有2个长得一样的元素、图3有2个长得一样的元素。
②相邻找相同:看图1和图2、图2和图3有没有相同的元素。
3.颜色不同,一般为两种,如图二,图(1)的黑色和白色看作两种元素;大小不同,一般为一种,图(2)的大圆和小圆看作一种元素。
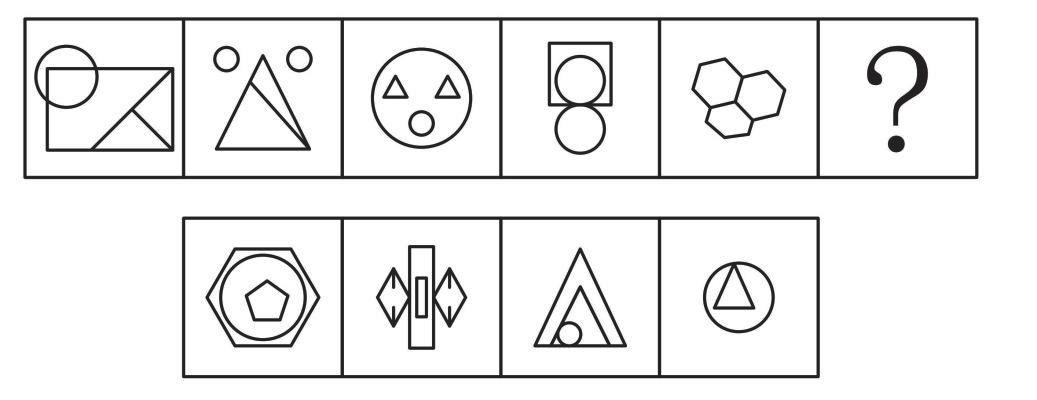
【例1】(2023事业单位)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】
1.出现小元素,考虑元素的种类和个数,题干和选项都有6个图形,元素个数选不出答案;题干每幅图都有3种元素。
B项:有4种元素,排除。
A、C、D项:有3种元素,均保留。
元素的细化考虑找相同的元素,可以在内部找相同,也可以相邻找相同。如先看内部,图1有3个三角形、2个椭圆、1个平行四边形,图2有3个“L”形、2个三角形、1个圆形,题干每幅图的相同元素均为“3、2、1”分布,但无法排除选项;再相邻找相同,图1中3个的三角形到图2中变成2个,图2中3个的相同元素到图3中变成2个,图3中3个的相同元素到图4中变成2个,则图4中3个的相同元素(类似圆形)到“?”处应该变成2个,排除D项。
题干图形中3个的相同元素的位置是固定的,都是右上角、左下角、右下角,排除C项,选择A项。【选A】
【注意】
1.出现独立小元素——元素的种类和个数。
2.元素细化——找相同。
素的特殊考点:部分数
1.什么是部分数?连在一起就是一部分

2.什么时候考虑部分数?生活化、粗线条图形

【例2】(2021江苏)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
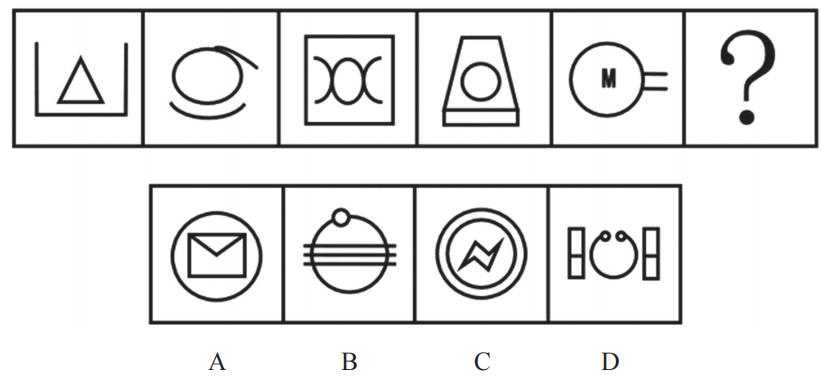
【解析】2.题干不好识别考点,选项更好识别,D项类似“螃蟹”,C项类似“闪电、充电的标志”,A项类似“信封”,图5的“M”是生活化图形,出现生活化图形、粗线条图形,考虑部分数。题干图形均为2部分,则“?”处图形应为2部分。
A项:有2个部分,保留。
B项:有1个部分,排除。
C、D项:有3个部分,均排除。【选A】
【注意】生活化、粗线条——数部分数。
生活化、粗线条图形常见考法:
1.属性(对称、开闭、曲直)

图一
2.部分数

图二
图三
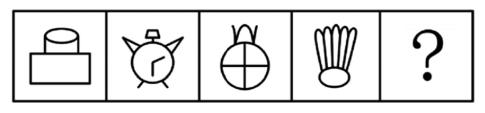
【注意】生活化、粗线条图形常见考法:按照考频高低排序,可以按照顺序尝试。
1.属性(对称、开闭、曲直):如图一,“5”不对称,均为全开放图形。
2.部分数:如图二,部分数依次为1、2、3、4、5。
3.面数量:如图三,面数量依次为3、4、5、6。
4.图三可以考查曲直,但图一、图二无法考查曲直,因为黑色部分的里面不算是线条,线条指的是细的,黑色图形一般不会考查曲直性。
5.答疑:以上可以考查对称,但对称性没有规律。

考点五:数量规律的复合考法
【例1】(2021四川下)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】1.每幅图都出现“窟窿”,可能考虑数面,题干图形的面数量依次为3、4、3、6、5,没有规律,面的细化(三角形面、相同面、最大/最小面)也没有规律。数面没有规律,但是出现重复的数字,一般情况下会考查面数量和外框复合,外框的边数量依次为3、4、3、6、5,规律为面数量=外框边数量。
A项:面数量为3,外框边数量为4,排除。
B项:面数量为4,外框边数量为7,排除。
C项:面数量为4,外框边数量为4,当选。
D项:面数量为3,外框边数量太多了,排除。 答疑:图3明显不对称,无法考查对称性。【选C】
【注意】 1.图形被分割、封闭面明显——面数量。
2.面数量有重复——面与外框复合。考试一般考查三角形到八边形,基本不 会考到九边形,3~8一共6个数字,题干一共6幅图,那么应该是三角形、四边形、五边形、六边形、七边形、八边形,直接考查即可,不需要考查复合;一般都考不到八边形,基本考的都是三边形到六边形,一共4个数字,而题干一共6幅图,那么这4个数字一定会有重复,面数量有重复,就会结合外框考查。
面数量有重复——面与外框复合
【2021江苏】面=外框
题干图形的面数量依次为3、4、4、5、3,面数量出现重复,考虑面与外框边数量复合,外框边数量依次为3、4、4、5、3,面数量=外框边数量,选择A项。
【2024浙江】面=外框
题干图形的面数量依次为3、5、4、5、6,面数量出现重复,考虑面与外框复合,外框边数量依次为3、5、4、5、6,面数量=外框边数量,选择A项。
2021江苏的图1和2024浙江的图1存在特征,考查面数量与外框复合时,图1特别喜欢用三角形。
【例2】(2020国考)
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
【解析】2.每幅图都有曲有直,考虑切点、曲直交点,图1没有切点,则考虑曲直交点;题干图形的曲直交点数依次为4、6、2……,没有规律。
每幅图都有曲有直,而且切点没有规律,考虑曲直交点、曲线、直线。曲直交点数依次为4、6、2、4、8;曲线数依次为2、3、1、2、4,规律为曲直交点数=2倍的曲线数,选项都是1条曲线,则找有2个曲直交点的选项。
A项:4个曲直交点,排除。
B项:4个曲直交点,排除。
C项:1个曲直交点,排除。
D项:2个曲直交点,当选。【选D】
【注意】
1.每个图都有曲有直——切点、曲直交点。
2.每个图都有曲有直且切点没规律——曲直交点、曲线、直线。
每个图都有曲有直且切点没规律——曲直交点、曲线、直线
【2023北京】直线-曲线=2、1、0。1、0、-1
【2020国考】曲直交点是曲线数的2倍
【注意】如2023北京和2020国考,每个图都有曲有直且切点没规律,则数曲直交点、曲线、直线,互相做运算。
1.2020国考:曲直交点是曲线数的2倍。
2.2023北京:直线和曲线做运算,第一组图中直线-曲线=2、1、0,第二组图中直线-曲线=1、0、-1,都是等差的。
元素组成相同——位置(平移、旋转、翻转)
元素组成相似——样式(加减同异、黑白运算)
元素组成不同——先属性(对称、曲直、开闭)
——后数量(点、线、角、面、素)
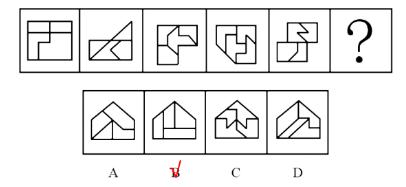
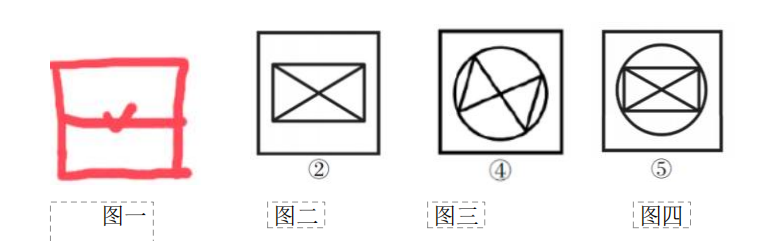
测验1.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
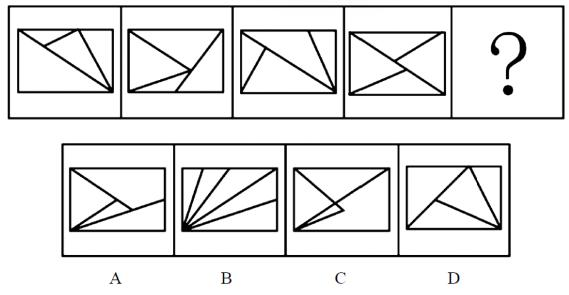
【解析】测验1.每幅图都是长方形内部被分割,考虑数面,题干都是4个面,则“?”处图形应有4个面。
B项:有5个面,排除。
面的细化考虑三角形面、相同面、最大/最小面,题干全部都是三角形面,选择D项。【选D】
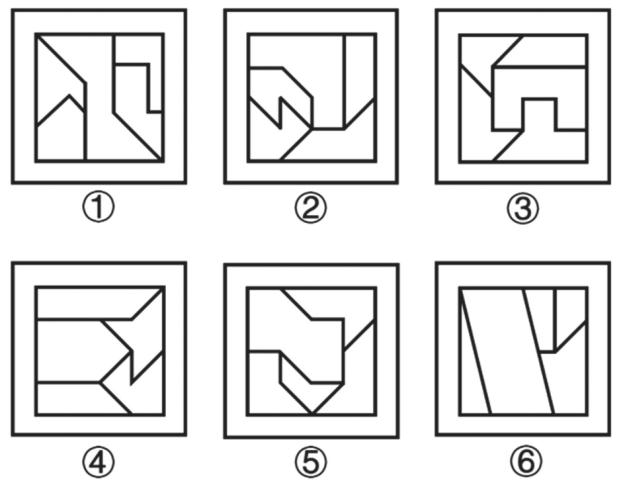
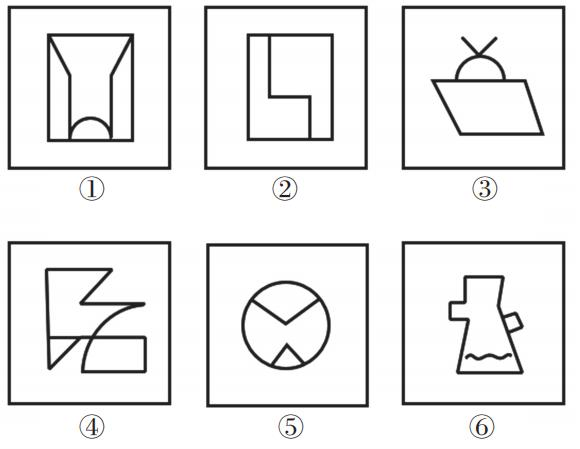
测验2.把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
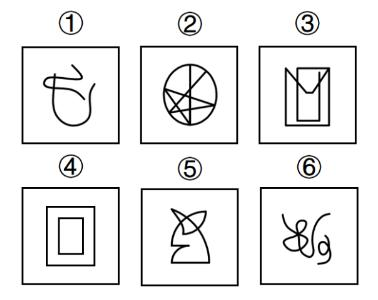
A.①②③,④⑤⑥
B.①④⑥,②③⑤
C.①②⑤,③④⑥
D.①②⑥,③④⑤
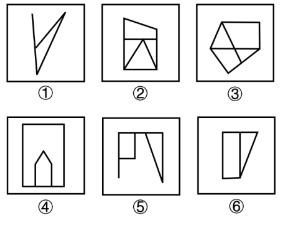
【解析】测验2.图①③⑥出现出头端点,图②内部类似五角星,考虑笔画数。
图①④⑥为一组,均为两笔画;图②③⑤为一组,均为一笔画,选择B项。【选B】
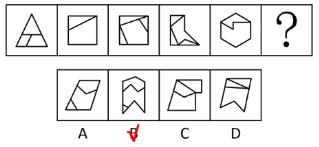
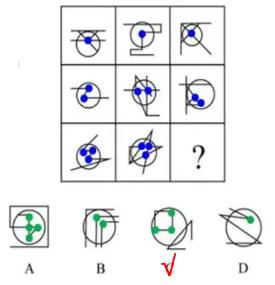
测验3.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
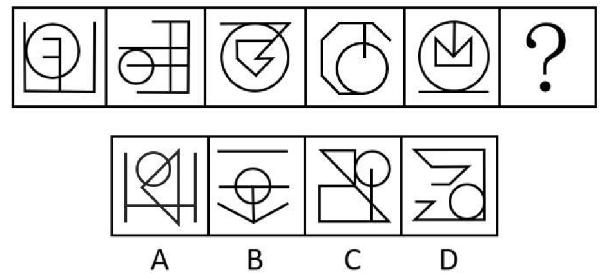
【解析】测验3.每幅图都有圆形,优先考虑切点,其次圆上/圆内交点,最后曲直交点。题干每幅图都有1个切点,则“?”处图形应有1个切点,选择C项。
A、B项:没有切点,均排除。
D项:有2个切点,排除。【选C】